
【題目】已知函數f(x)=|cosx|sinx,給出下列五個說法:
①f( ![]() π)=﹣
π)=﹣ ![]() ;
;
②若|f(x1)|=|f(x2)|,則x1=x2+kπ(k∈Z);
③f(x)在區間[﹣ ![]() ,
, ![]() ]上單調遞增;
]上單調遞增;
④函數f(x)的周期為π.
⑤f(x)的圖象關于點( ![]() ,0)成中心對稱.
,0)成中心對稱.
其中正確說法的序號是 .
【答案】①③
【解析】解:由題意函數f(x)=|cosx|sinx= 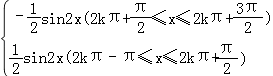 (k∈Z);
(k∈Z);
對于①:f( ![]() π)=|cos
π)=|cos ![]() |sin
|sin ![]() =)=|cos(
=)=|cos( ![]() )|sin(27π
)|sin(27π ![]() )=
)= ![]() =﹣
=﹣ ![]() ;所以①對
;所以①對
對于②:若|f(x1)|=|f(x2)|,當x2= ![]() ,x1=
,x1= ![]() 時,成立,則x1=x2+
時,成立,則x1=x2+ ![]() ,所以②不對
,所以②不對
對于③f(x)在區間[﹣ ![]() ,
, ![]() ]上時,f(x)=
]上時,f(x)= ![]() sin2x,可得2x∈[-
sin2x,可得2x∈[- ![]() ,
, ![]() ],x∈[﹣
],x∈[﹣ ![]() ,
, ![]() ]上是單調遞增;所以③對.
]上是單調遞增;所以③對.
對于④:函數f(x)=|cosx|sinx,則f(x+π)=|cos(x+π)|sin(x+π)=﹣(|cosx|sinx)=﹣f(x),可得函數f(x)的周期不是π.所以④不對.
對于⑤:由于f( ![]() )=|cos(x+
)=|cos(x+ ![]() )|sin(x+
)|sin(x+ ![]() )=cosx|sinx|,f(
)=cosx|sinx|,f( ![]() )=|cos(﹣x+
)=|cos(﹣x+ ![]() )|sin(﹣x+
)|sin(﹣x+ ![]() )=cosx|sinx|
)=cosx|sinx|
則:f( ![]() )=f(
)=f( ![]() )圖象關于x=
)圖象關于x= ![]() 對稱.所以⑤不對.
對稱.所以⑤不對.
綜上所得:①③正確,②④⑤不對.
所以答案是:①③.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】如圖,四棱錐P-ABCD中,側面PAD為等邊三角形且垂直于底面ABCD,AB=BC=![]() AD,∠BAD=∠ABC=90°,E是PD的中點.
AD,∠BAD=∠ABC=90°,E是PD的中點.
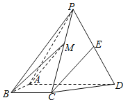
(1)證明:直線CE∥平面PAB;
(2)點M在棱PC上,且直線BM與底面ABCD所成角為45°,求二面角M-AB-D的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】甲、乙兩人進行某項對抗性游戲,采用“七局四勝”制,即先贏四局者為勝,若甲、乙兩人水平相當,且已知甲先贏了前兩局.
![]() Ⅰ
Ⅰ![]() 求乙取勝的概率;
求乙取勝的概率;
![]() Ⅱ
Ⅱ![]() 記比賽局數為X,求X的分布列及數學期望
記比賽局數為X,求X的分布列及數學期望![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某學校青年職工、中年職工、老年職工的人數之比為7:5:3,為了了解該單位職工的健康情況,用分層抽樣的方法從中抽取樣本 .若樣本中的青年職工為14人,則樣本容量為______.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=|x﹣10|+|x﹣20|,且滿足f(x)<10a+10(a∈R)的解集不是空集.
(Ⅰ)求實數a的取值集合A
(Ⅱ)若b∈A,a≠b,求證aabb>abba .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】北京市環境保護監測中心每月向公眾公布北京市各區域的空氣質量狀況![]() 年1月份各區域的
年1月份各區域的![]() 濃度情況如表:
濃度情況如表:
各區域1月份![]() 濃度
濃度![]() 單位:微克
單位:微克![]() 立方米
立方米![]() 表
表
區域 |
| 區域 |
| 區域 |
|
懷柔 | 27 | 海淀 | 34 | 平谷 | 40 |
密云 | 31 | 延慶 | 35 | 豐臺 | 42 |
門頭溝 | 32 | 西城 | 35 | 大興 | 46 |
順義 | 32 | 東城 | 36 | 開發區 | 46 |
昌平 | 32 | 石景山 | 37 | 房山 | 47 |
朝陽 | 34 | 通州 | 39 |
從上述表格隨機選擇一個區域,其2018年1月份![]() 的濃度小于36微克
的濃度小于36微克![]() 立方米的概率是
立方米的概率是![]()
![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設f(x)=|ax﹣2|.
(1)若關于x的不等式f(x)<3的解集為(﹣ ![]() ,
, ![]() ),求a的值;
),求a的值;
(2)f(x)+f(﹣x)≥a對于任意x∈R恒成立,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=2x+2﹣x .
(1)求方程f(x)= ![]() 的根;
的根;
(2)求證:f(x)在[0,+∞)上是增函數;
(3)若對于任意x∈[0,+∞),不等式f(2x)≥f(x)﹣m恒成立,求實數m的最小值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com