【題目】某學(xué)校青年職工、中年職工、老年職工的人數(shù)之比為7:5:3，為了了解該單位職工的健康情況，用分層抽樣的方法從中抽取樣本 ．若樣本中的青年職工為14人，則樣本容量為______．
【答案】30
【解析】
根據(jù)給出的單位青年職工、中年職工、老年職工的人數(shù)之比為7：5：3，得到青年職工在單位所占的人數(shù)比例，從而得到中年職工和老年職工的人數(shù)和所占的比例，運(yùn)用分層抽樣中每層所抽取的比例相等，求該單位中年職工和老年職工被抽取的人數(shù)和．
因?yàn)閱挝恢星嗄曷毠ぁ⒅心曷毠ぁ⒗夏曷毠さ娜藬?shù)之比為7：5：3，所以青年職工所占人數(shù)比例為
，
中年職工與老年職工的和所占人數(shù)比例為
，
設(shè)樣本中中年職工和老年職工的人數(shù)和為m，
則
所以m=16，所以樣本容量為14+16=30．
故答案為：30.
第1卷單元月考期中期末系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦！ | 初一 | 初一免費(fèi)課程推薦！ |
| 高二 | 高二免費(fèi)課程推薦！ | 初二 | 初二免費(fèi)課程推薦！ |
| 高三 | 高三免費(fèi)課程推薦！ | 初三 | 初三免費(fèi)課程推薦！ |
科目：高中數(shù)學(xué) 來(lái)源： 題型：
【題目】已知A，B是橢圓 
=1和雙曲線 
=1的公共頂點(diǎn)，其中a＞b＞0，P是雙曲線上的動(dòng)點(diǎn)，M是橢圓上的動(dòng)點(diǎn)（P，M都異于A，B），且滿足 
=λ（ 
）（λ∈R），設(shè)直線AP，BP，AM，BM的斜率分別為k1 ， k2 ， k3 ， k4 ， 若k1+k2= 
，則k3+k4= ．
查看答案和解析>>
科目：高中數(shù)學(xué) 來(lái)源： 題型：
【題目】若方程|x2﹣2x﹣1|﹣t=0有四個(gè)不同的實(shí)數(shù)根x1、x2、x3、x4，且x1＜x2＜x3＜x4 ， 則2（x4﹣x1）+（x3﹣x2）的取值范圍是（ ）
A.（8，6 
）
B.（6 ，4 
）
C.[8，4 ]
D.（8，4 ]
查看答案和解析>>
科目：高中數(shù)學(xué) 來(lái)源： 題型：
【題目】過(guò)拋物線C：y2=4x的焦點(diǎn)F作直線l交拋物線C于A，B，若|AF|=3|BF|，則l的斜率是
查看答案和解析>>
科目：高中數(shù)學(xué) 來(lái)源： 題型：
【題目】在極坐標(biāo)系中，圓
的方程為
，以坐標(biāo)原點(diǎn)為極點(diǎn)，
軸正半軸為極軸建立極坐標(biāo)系，直線
的參數(shù)方程為
（
為參數(shù)）
（1）求圓的直角坐標(biāo)方程和直線的普通方程；
（2）若直線與圓相切，求實(shí)數(shù)
的值；
查看答案和解析>>
科目：高中數(shù)學(xué) 來(lái)源： 題型：
【題目】全世界越來(lái)越關(guān)注環(huán)境保護(hù)問(wèn)題，某監(jiān)測(cè)站點(diǎn)于2018年1月某日起連續(xù)
天監(jiān)測(cè)空氣質(zhì)量指數(shù)(
)，數(shù)據(jù)統(tǒng)計(jì)如下：
空氣質(zhì)量指數(shù)( |
|
|
|
|
|
空氣質(zhì)量等級(jí) | 空氣優(yōu) | 空氣良 | 輕度污染 | 中度污染 | 重度污染 |
天數(shù) | 20 | 40 |
| 10 | 5 |
（1）根據(jù)所給統(tǒng)計(jì)表和頻率分布直方圖中的信息求出，
的值，并完成頻率分布直方圖；
（2）由頻率分布直方圖，求該組數(shù)據(jù)的眾數(shù)和中位數(shù)；
（3）在空氣質(zhì)量指數(shù)分別屬于
和
的監(jiān)測(cè)數(shù)據(jù)中，用分層抽樣的方法抽取
天，再?gòu)闹腥我膺x取
天，求事件
“兩天空氣都為良”發(fā)生的概率.
查看答案和解析>>
科目：高中數(shù)學(xué) 來(lái)源： 題型：
【題目】已知函數(shù)f（x）=|cosx|sinx，給出下列五個(gè)說(shuō)法：
①f（ 
π）=﹣ 
；
②若|f（x1）|=|f（x2）|，則x1=x2+kπ（k∈Z）；
③f（x）在區(qū)間[﹣ 
， ]上單調(diào)遞增；
④函數(shù)f（x）的周期為π．
⑤f（x）的圖象關(guān)于點(diǎn)（ 
，0）成中心對(duì)稱．
其中正確說(shuō)法的序號(hào)是 ．
查看答案和解析>>
科目：高中數(shù)學(xué) 來(lái)源： 題型：
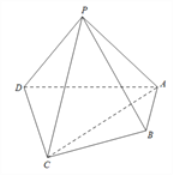
【題目】如圖，在四棱錐
中，平面PAD⊥平面ABCD，PA⊥PD，PA=PD，AB⊥AD，AB=1，AD=2， 
.
（1）求證：PD⊥平面PAB；
（2）求直線PB與平面PCD所成角的正弦值.
查看答案和解析>>
科目：高中數(shù)學(xué) 來(lái)源： 題型：
【題目】對(duì)某交通要道以往的日車流量（單位：萬(wàn)輛）進(jìn)行統(tǒng)計(jì)，得到如下記錄：
日車流量x | 0≤x＜5 | 5≤x＜10 | 10≤x＜15 | 15≤x＜20 | 20≤x＜25 | x≥25 |
頻率 | 0.05 | 0.25 | 0.35 | 0.25 | 0.10 | 0 |
將日車流量落入各組的頻率視為概率，并假設(shè)每天的車流量相互獨(dú)立．
（1）求在未來(lái)連續(xù)3天里，有連續(xù)2天的日車流量都不低于10萬(wàn)輛且另1天的日車流量低于5萬(wàn)輛的概率；
（2）用X表示在未來(lái)3天時(shí)間里日車流量不低于10萬(wàn)輛的天數(shù)，求X的分布列和數(shù)學(xué)期望．
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話：027-86699610 舉報(bào)郵箱：58377363@163.com
