
【題目】中國古代十進制的算籌計數法,在數學史上是一個偉大的創造.根據史書的記載和考古材料的發現,古代的算籌實際上是一根根同樣長短和粗細的小棍子,一般長為![]() ,徑粗
,徑粗![]() ,多用竹子制成,也有用木頭、獸骨、象牙、金屬等材料制成的,大約二百七十幾枚為一束,放在一個布袋里,系在腰部隨身攜帶.需要記數和計算的時候,就把它們取出來,放在桌上、炕上或地上都能擺弄.在算籌計數法中,以縱橫兩種排列方式來表示數字.如圖,是利用算籌表示數1~9的一種方法.例如:3可表示為“
,多用竹子制成,也有用木頭、獸骨、象牙、金屬等材料制成的,大約二百七十幾枚為一束,放在一個布袋里,系在腰部隨身攜帶.需要記數和計算的時候,就把它們取出來,放在桌上、炕上或地上都能擺弄.在算籌計數法中,以縱橫兩種排列方式來表示數字.如圖,是利用算籌表示數1~9的一種方法.例如:3可表示為“![]() ”,26可表示為“
”,26可表示為“![]() ”,現有6根算籌,據此表示方法,若算籌不能剩余,則用這6根算籌能表示的兩位數的個數為( )
”,現有6根算籌,據此表示方法,若算籌不能剩余,則用這6根算籌能表示的兩位數的個數為( )
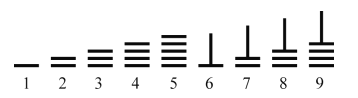
A.13B.14C.15D.16
科目:高中數學 來源: 題型:
【題目】函數f(x)=Asin(wx+j)(A>0,w>0,-![]() <j<
<j<![]() ,x∈R)的部分圖象如圖所示:
,x∈R)的部分圖象如圖所示: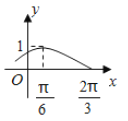 ,
,
(1)求函數y=f(x)的解析式;(2)當x∈![]() 時,求f(x)的取值范圍.
時,求f(x)的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】ΔABC的內角A,B,C的對邊分別為a,b,c,根據下列條件解三角形,其中有兩解的是
A. a=2,b=3,A=30°B. b=6,c=4,A=120°
C. a=4![]() ,b=6,A=60°D. a=3,b=6,A=30°
,b=6,A=60°D. a=3,b=6,A=30°
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=![]() sin(ωx-
sin(ωx-![]() )(其中ω>0)的圖象上相鄰兩個最高點的距離為π.
)(其中ω>0)的圖象上相鄰兩個最高點的距離為π.
(Ⅰ)求函數f(x)的圖象的對稱軸;
(Ⅱ)若函數y=f(x)-m在[0,π]內有兩個零點x1,x2,求m的取值范圍及cos(x1+x2)的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖1,在梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 的中點,
的中點,![]() 是
是![]() 與
與![]() 的交點,以
的交點,以![]() 為折痕把
為折痕把![]() 折起,使點
折起,使點![]() 到達點
到達點![]() 的位置,且
的位置,且![]() ,如圖2.
,如圖2.
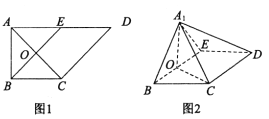
(1)證明:平面![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了適應高考改革,某中學推行“創新課堂”教學.高一平行甲班采用“傳統教學”的教學方式授課,高一平行乙班采用“創新課堂”的教學方式授課,為了比較教學效果,期中考試后,分別從兩個班中各隨機抽取![]() 名學生的成績進行統計分析,結果如下表:(記成績不低于
名學生的成績進行統計分析,結果如下表:(記成績不低于![]() 分者為“成績優秀”)
分者為“成績優秀”)
分數 |
|
|
|
|
|
|
|
甲班頻數 |
|
|
|
|
|
|
|
乙班頻數 |
|
|
|
|
|
|
|
(1)由以上統計數據填寫下面的![]() 列聯表,并判斷是否有
列聯表,并判斷是否有![]() 以上的把握認為“成績優秀與教學方式有關”?
以上的把握認為“成績優秀與教學方式有關”?
甲班 | 乙班 | 總計 | |
成績優秀 | |||
成績不優秀 | |||
總計 |
(2)在上述樣本中,學校從成績為![]() 的學生中隨機抽取
的學生中隨機抽取![]() 人進行學習交流,求這
人進行學習交流,求這![]() 人來自同一個班級的概率.
人來自同一個班級的概率.
參考公式:![]() ,其中
,其中![]() .
.
臨界值表
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某城市為了解游客人數的變化規律,提高旅游服務質量,收集并整理了2015年1月至2017年12月期間月接待游客量(單位:萬人)的數據,繪制了下面的折線圖.根據該折線圖,下列結論錯誤的是()
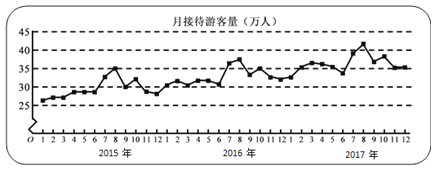
A. 年接待游客量逐年增加
B. 各年的月接待游客量高峰期在8月
C. 2015年1月至12月月接待游客量的中位數為30萬人
D. 各年1月至6月的月接待游客量相對于7月至12月,波動性更小,變化比較平穩
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com