Question

【題目】已知函數(shù)f(x)是定義在R上的奇函數(shù)，當(dāng)x>0時，f(x)＝log2x.

(1)求f(x)的解析式；

(2)解關(guān)于x的不等式f(x)≤ .

Answer 1

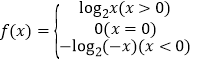【答案】（1） （2）

【解析】

（1）設(shè)x＜0，則﹣x＞0，由x＞0時的解析式和函數(shù)的奇偶性可得到函數(shù)解析式（2）根據(jù)（1）中函數(shù)的解析式，分別解出各段上滿足f(x)≤的x范圍，然后取并集即可.

（1）設(shè)x＜0，則﹣x＞0，∵當(dāng)x＞0時，f（x）＝log2x

∴f（﹣x）＝log2（﹣x），又∵函數(shù)f（x）是奇函數(shù)

∴f（x）＝﹣f（﹣x）＝﹣log2（﹣x）．

當(dāng)x＝0時，f（0）＝0

綜上所述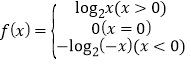

（2）由（1）得不等式f(x)≤ 可化為

x＞0時，，解得0＜x≤

x＝0時，0≤，滿足條件，

x＜0時，，解得x≤，

綜上所述原不等式的解集為.