
【題目】已知函數f(x)=x(e![]() +1)
+1)
(I)求函數y=f(x)的圖象在點(0,f(0))處的切線方程;
(II)若函數g(x)=f(x)-ae![]() -x,求函數g(x)在[1,2]上的最大值。
-x,求函數g(x)在[1,2]上的最大值。
【答案】(1)y=2x(2)見解析
【解析】試題分析:(1)先根據導數幾何意義求切線斜率,再根據點斜式得切線方程,(2)先求導數,再求導函數零點,根據零點與定義區間相對位置關系確定函數單調性,最后根據單調性確定函數最大值取法.
試題解析:解:(I)依題意,f(x)=e![]() +1+xe
+1+xe![]() ,故f(0)=e
,故f(0)=e![]() +1=2.
+1=2.
因為f(0)=0,故所求切線方程為y=2x;.
(Ⅱ)依題意,g(x)=(x-a+1)·e![]() ,令g(x)=0得x=a-1
,令g(x)=0得x=a-1
所以當a-1≤1時,x∈[1,2]時,g(x)≥0恒成立,g(x)單調遞增,g(x)最大值為g(2),.
當a-1≥2時,x∈[1,2]時,g(x)≤0恒成立,g(x)單調遞減,g(x)最大值為g(1).
當1<a-1<2時,x∈[1,a-1)時,g(x)≤0,g(x)單調遞減;
x∈(a-1,2)時,g(x)>0,g(x)單調遞增.
當x∈[1,2]時,g(x)最大值為g(1)或g(2).
g(1)=(1-a)e,g(2)=(2-a)e![]() ,
,
g(1)-g(2)=(1-a)e-(2-a)e![]() =(e
=(e![]() -e)a-(2e
-e)a-(2e![]() -e).
-e).
∴當![]() 時,g(1)-g(2)≥0,g(x)max=g(1)=(1-a)e.
時,g(1)-g(2)≥0,g(x)max=g(1)=(1-a)e.
當a<![]() =
=![]() 時,g(1)-g(2)<0,g(x)max=g(2)=(2-a)e
時,g(1)-g(2)<0,g(x)max=g(2)=(2-a)e![]()


科目:高中數學 來源: 題型:
【題目】對于給定的正整數![]() ,若數列
,若數列![]() 滿足
滿足![]() 對任意正整數
對任意正整數![]() 總成立,則稱數列
總成立,則稱數列![]() 是“
是“![]() 數列”.
數列”.
(1)證明:等差數列![]() 是“
是“![]() 數列”;
數列”;
(2)若數列![]() 既是“
既是“![]() 數列”,又是“
數列”,又是“![]() 數列”,證明:
數列”,證明: ![]() 是等差數列.
是等差數列.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(本小題滿分12分)已知在四棱錐![]() 中,底面
中,底面![]() 是矩形,且
是矩形,且![]() ,
,![]() ,
,![]() 平面
平面![]() ,
,![]() ,
,![]() 分別是線段
分別是線段![]() ,
,![]() 的中點.
的中點.
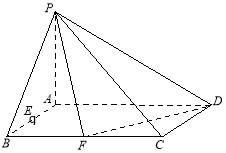
(1)判斷并說明![]() 上是否存在點
上是否存在點![]() ,使得
,使得![]() 平面
平面![]() ?若存在,求出
?若存在,求出![]() 的值;若不
的值;若不
存在,請說明理由;
(2)若![]() 與平面
與平面![]() 所成的角為
所成的角為![]() ,求二面角
,求二面角![]() 的平面角的余弦值.
的平面角的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標坐標系![]() 中,過點P(1,0)的直線l的參數方程為
中,過點P(1,0)的直線l的參數方程為![]() (
(![]() 為參數,
為參數, ![]() ),以坐標原點
),以坐標原點![]() 為極點,
為極點, ![]() 軸的正半軸為極軸建立極坐標系,已知頂點在極軸上,開口向右的拋物線C經過極坐標為(2,
軸的正半軸為極軸建立極坐標系,已知頂點在極軸上,開口向右的拋物線C經過極坐標為(2, ![]() )的點Q.
)的點Q.
(1)求C的極坐標方程;
(2)若l與C交于A、B兩點,且|PA|=2|PB|,求tan![]() 的值。
的值。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,矩形ADEF與梯形ABCD所在的平面互相垂直,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,M為CE的中點,N為CD中點.
,M為CE的中點,N為CD中點.
![]() 求證:平面
求證:平面![]() 平面ADEF;
平面ADEF;
![]() 求證:平面
求證:平面![]() 平面BDE;
平面BDE;
![]() 求點D到平面BEC的距離.
求點D到平面BEC的距離.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】[選修4一4:坐標系與參數方程]已知直線l過原點且傾斜角為![]() ,
, ![]()
![]()
![]() ,以原點O為極點,x軸的非負半軸為極軸建立極坐標系,曲線C 的極坐標方程為psin
,以原點O為極點,x軸的非負半軸為極軸建立極坐標系,曲線C 的極坐標方程為psin![]()
![]() =4cos
=4cos![]() .
.
(I)寫出直線l的極坐標方程和曲線C 的直角坐標方程;
(Ⅱ)已知直線l過原點且與直線l相互垂直,若l![]() C=-M,l
C=-M,l![]() C=N,其中M,N不與原點重合,求△OMN 面積的最小值.
C=N,其中M,N不與原點重合,求△OMN 面積的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某集團為了獲得更大的收益,每年要投入一定的資金用于廣告促銷.經調查投入廣告費t(百萬元),可增加銷售額約為-t2+5t(百萬元)(0≤t≤5) (注:收益=銷售額-投放).
(1)若該公司將當年的廣告費控制在3百萬元之內,則應投入多少廣告費,才能使該公司由此獲得的收益最大?
(2)現該公司準備共投入3百萬元,分別用于廣告促銷和技術改造.經預測,每投入技術改造費x(百萬元),可增加的銷售額約為-![]() x3+x2+3x(百萬元).請設計一個資金分配方案,使該公司由此獲得的收益最大.
x3+x2+3x(百萬元).請設計一個資金分配方案,使該公司由此獲得的收益最大.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】一年來,某足球隊的![]() 足球運動員每天進行距離球門
足球運動員每天進行距離球門![]() 米遠的射門訓練
米遠的射門訓練![]() 次,若打進球門算成功,否則算失敗.隨機提取該球員連續
次,若打進球門算成功,否則算失敗.隨機提取該球員連續![]() 天的成功次數統計如下:
天的成功次數統計如下:
![]() .
.
(1)估計該球員一天射門成功次數的四分位數;
(2)若每天![]() 三位球員均進行“三角戰術”配合訓練,要求三位球員在運動中必須保持如下規則:三人所在的位置構成
三位球員均進行“三角戰術”配合訓練,要求三位球員在運動中必須保持如下規則:三人所在的位置構成![]() ,
,![]() ,
,![]() 的面積
的面積![]() (平方米).求
(平方米).求![]() 球員之間的距離的最小值(米).
球員之間的距離的最小值(米).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】現安排甲、乙、丙、丁、戊5名同學參加2022年杭州亞運會志愿者服務活動,有翻譯、導游、禮儀、司機四項工作可以安排,以下說法正確的是( )
A. 每人都安排一項工作的不同方法數為![]()
B. 每項工作至少有一人參加,則不同的方法數為![]()
C. 如果司機工作不安排,其余三項工作至少安排一人,則這5名同學全部被安排的不同方法數為![]()
D. 每項工作至少有一人參加,甲、乙不會開車但能從事其他三項工作,丙、丁、戊都能勝任四項工作,則不同安排方案的種數是![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com