
【題目】已知函數 ![]() (其中
(其中 ![]() ,
, ![]() 為常數,
為常數, ![]() 為自然對數的底數).
為自然對數的底數).
(1)討論函數 ![]() 的單調性;
的單調性;
(2)設曲線 ![]() 在
在 ![]() 處的切線為
處的切線為 ![]() ,當
,當 ![]() 時,求直線
時,求直線 ![]() 在
在 ![]() 軸上截距的取值范圍.
軸上截距的取值范圍.
【答案】
(1)解: ![]() ,
,
當 ![]() 時,
時, ![]() 恒成立,函數
恒成立,函數 ![]() 的遞增區間是
的遞增區間是 ![]() ;
;
當 ![]() 時,
時, ![]() 或
或 ![]() .
.
函數 ![]() 的遞增區間是
的遞增區間是 ![]() ,
, ![]() ,遞減區間是
,遞減區間是 ![]()
(2)解: ![]() ,
, ![]() ,
,
所以直線 ![]() 的方程為:
的方程為: ![]() .
.
令 ![]() 得到:截距
得到:截距 ![]() ,記
,記 ![]() ,
,![]() ,記
,記 ![]()
![]() (∵
(∵ ![]() ),所以
),所以 ![]() 遞減,
遞減,
∴ ![]() ,∴
,∴ ![]() ,即
,即 ![]() 在區間
在區間 ![]() 上單調遞減,
上單調遞減,
∴ ![]() ,即截距的取值范圍是:
,即截距的取值范圍是: ![]() .
.
【解析】(1)求復合函數的單調性要先對函數進行求導,找到導函數的零點,再根據“導函數大于0,原函數單調遞增,小于0,原函數單調遞減”,進一步判斷函數的單調區間。
(2)先設出切線l,再根據函數的性質確定b的取值范圍。設切線時要注意直線方程的選取,已知直線上一點和其斜率,可直接設點斜式;在求b時,要注意a的取值范圍。
【考點精析】通過靈活運用函數單調性的判斷方法和復合函數單調性的判斷方法,掌握單調性的判定法:①設x1,x2是所研究區間內任兩個自變量,且x1<x2;②判定f(x1)與f(x2)的大小;③作差比較或作商比較;復合函數f[g(x)]的單調性與構成它的函數u=g(x),y=f(u)的單調性密切相關,其規律:“同增異減”即可以解答此題.


 字詞句篇與同步作文達標系列答案
字詞句篇與同步作文達標系列答案科目:高中數學 來源: 題型:
【題目】為對考生的月考成績進行分析,某地區隨機抽查了 ![]() 名考生的成績,根據所得數據畫了如下的樣本頻率分布直方圖.
名考生的成績,根據所得數據畫了如下的樣本頻率分布直方圖.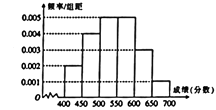
(1)求成績在 ![]() 的頻率;
的頻率;
(2)根據頻率分布直方圖算出樣本數據的中位數;
(3)為了分析成績與班級、學校等方面的關系,必須按成績再從這 ![]() 人中用分層抽樣方法抽取出
人中用分層抽樣方法抽取出 ![]() 人作出進一步分析,則成績在
人作出進一步分析,則成績在 ![]() 的這段應抽多少人?
的這段應抽多少人?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在等腰直角△ABO中,設 ![]() =
= ![]() ,
, ![]() =
= ![]() ,|
,| ![]() |=|
|=| ![]() |=1,C為AB上靠近A點的三等分點,過C作AB的垂線l,設P為垂線上任一點,
|=1,C為AB上靠近A點的三等分點,過C作AB的垂線l,設P為垂線上任一點, ![]() =
= ![]() ,則
,則 ![]() (
( ![]() ﹣
﹣ ![]() )=( )
)=( ) 
A.![]()
B.﹣ ![]()
C.﹣ ![]()
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某人到甲、乙兩市各 ![]() 個小區調查空置房情況,調查得到的小區空置房的套數繪成了如圖的莖葉圖,則調查中甲市空置房套數的中位數與乙市空置房套數的中位數之差為( )
個小區調查空置房情況,調查得到的小區空置房的套數繪成了如圖的莖葉圖,則調查中甲市空置房套數的中位數與乙市空置房套數的中位數之差為( )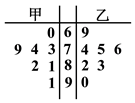
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖, ![]() 為圓柱
為圓柱 ![]() 的母線,
的母線, ![]() 是底面圓
是底面圓 ![]() 的直徑,
的直徑, ![]() 是
是 ![]() 的中點.
的中點.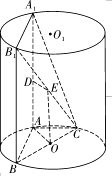
(Ⅰ)問: ![]() 上是否存在點
上是否存在點 ![]() 使得
使得 ![]() 平面
平面 ![]() ?請說明理由;
?請說明理由;
(Ⅱ)在(Ⅰ)的條件下,若 ![]() 平面
平面 ![]() ,假設這個圓柱是一個大容器,有條體積可以忽略不計的小魚能在容器的任意地方游弋,如果小魚游到四棱錐
,假設這個圓柱是一個大容器,有條體積可以忽略不計的小魚能在容器的任意地方游弋,如果小魚游到四棱錐 ![]() 外會有被捕的危險,求小魚被捕的概率.
外會有被捕的危險,求小魚被捕的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
在直角坐標系 ![]() 中,直線
中,直線 ![]() 的參數方程為
的參數方程為 ![]() (
( ![]() 為參數),直線
為參數),直線 ![]() 的參數方程為
的參數方程為  (
( ![]() 為參數),設
為參數),設 ![]() 與
與 ![]() 的交點為
的交點為 ![]() ,當
,當 ![]() 變化時,
變化時, ![]() 的軌跡為曲線
的軌跡為曲線 ![]() .
.
(1)寫出 ![]() 的普遍方程及參數方程;
的普遍方程及參數方程;
(2)以坐標原點為極點, ![]() 軸正半軸為極軸建立極坐標系,設曲線
軸正半軸為極軸建立極坐標系,設曲線 ![]() 的極坐標方程為
的極坐標方程為 ![]() ,
, ![]() 為曲線
為曲線 ![]() 上的動點,求點
上的動點,求點 ![]() 到
到 ![]() 的距離的最小值.
的距離的最小值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com