【題目】已知函數
.
（Ⅰ）求
的單調區間；
（Ⅱ）設
，若對任意
，均存在
使得
，求
的取值范圍.
【答案】（Ⅰ）見解析；（Ⅱ）
【解析】
(Ⅰ)首先求得導函數的解析式，然后結合函數的定義域和導函數的符號分類討論即可確定函數的單調區間；
(Ⅱ)首先求得函數
的最大值，然后進行等價轉化，結合(Ⅰ)中的結果分類討論即可確定
的取值范圍.
（Ⅰ）
.
①當
時，
，
，
在區間
上，
；在區間
上
，
故
的單調遞增區間是，單調遞減區間是.
②當
時，
，
在區間和
上，；在區間
上，
故的單調遞增區間是和，單調遞減區間是.
③當
時，
，故的單調遞增區間是
.
④當
時，
，在區間
和上，；區間
上，
故的單調遞增區間是和，單調遞減區間是.
（Ⅱ）設
，
，
，
為增函數，
由已知，
.據此可得
.
由（Ⅰ）可知，
①當
時，在
上單調遞增，
故
，
所以，
，解得，故
.
②當時，在
上單調遞增，在
上單調遞減，
故
.
由可知
，
，
，
所以，
，，
綜上所述，.
優百分課時互動系列答案科目：高中數學 來源： 題型：
【題目】如圖所示，在“楊輝三角”中，去除所有為1的項，依次構成數列2，3，3，4，6，4，5，10，10，5，…，則此數列前21項的和為_______________.
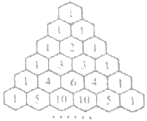
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某溫室大棚規定，一天中，從中午12點到第二天上午8點為保溫時段，其余4小時為工作作業時段，從中午12點連續測量20小時，得出此溫室大棚的溫度y（單位：度）與時間t（單位：小時，
）近似地滿足函數
關系，其中，b為大棚內一天中保溫時段的通風量。
（1）若一天中保溫時段的通風量保持100個單位不變，求大棚一天中保溫時段的最低溫度（精確到0.1℃）；
（2）若要保持一天中保溫時段的最低溫度不小于17℃，求大棚一天中保溫時段通風量的最小值。
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f(x)＝－
x3＋2x2＋2x，若存在滿足0≤x0≤3的實數x0，使得曲線y＝f(x)在點(x0，f(x0))處的切線與直線x＋my－10＝0垂直，則實數m的取值范圍是( )
A. [6，＋∞)B. (－∞，2]
C. [2,6]D. [5,6]
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】大數據時代對于現代人的數據分析能力要求越來越高，數據擬合是一種把現有數據通過數學方法來代入某條數式的表示方式，比如
，
，2，
，n是平面直角坐標系上的一系列點，用函數
來擬合該組數據，盡可能使得函數圖象與點列比較接近．其中一種描述接近程度的指標是函數的擬合誤差，擬合誤差越小越好，定義函數的擬合誤差為：
．已知平面直角坐標系上5個點的坐標數據如表：
x | 1 | 3 | 5 | 7 | 9 |
y | 12 |
| 4 |
| 12 |
若用一次函數
來擬合上述表格中的數據，求該函數的擬合誤差
的最小值，并求出此時的函數解析式
；
若用二次函數
來擬合題干表格中的數據，求
；
請比較第問中的
和第
問中的
，用哪一個函數擬合題目中給出的數據更好？
請至少寫出三條理由
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在四棱錐O﹣ABCD中，底面ABCD四邊長為1的菱形，∠ABC=
，OA⊥底面ABCD，OA=2，M為OA的中點，N為BC的中點．
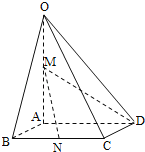
（1）證明：直線MN∥平面OCD；
（2）求異面直線AB與MD所成角的大小；
（3）求點B到平面OCD的距離．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
