
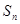 是各項均為非零實數的數列
是各項均為非零實數的數列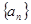 的前
的前 項和,給出如下兩個命題上:
項和,給出如下兩個命題上: :
: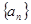 是等差數列;命題
是等差數列;命題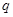 :等式
:等式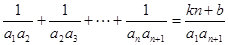 對任意
對任意 (
(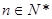 )恒成立,其中
)恒成立,其中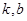 是常數。
是常數。 是
是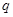 的充分條件,求
的充分條件,求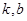 的值;
的值;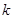 與
與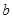 ,問
,問 是否為
是否為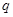 的必要條件,請說明理由;
的必要條件,請說明理由; 為真命題,對于給定的正整數
為真命題,對于給定的正整數 (
(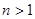 )和正數M,數列
)和正數M,數列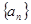 滿足條件
滿足條件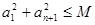 ,試求
,試求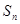 的最大值。
的最大值。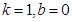 ;(2)是,證明見解析;(3)
;(2)是,證明見解析;(3)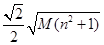 .
.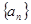 是等差數列,和
是等差數列,和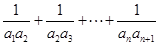 可以用裂項相消法求出,等式
可以用裂項相消法求出,等式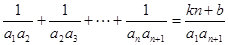 就變為關于
就變為關于 的恒等式,利用恒等式的知識可求出
的恒等式,利用恒等式的知識可求出 ;(2)等式
;(2)等式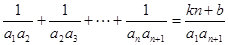 對任意
對任意 (
(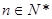 )恒成立,等式左邊是一個和式,相當于一個新數列的前
)恒成立,等式左邊是一個和式,相當于一個新數列的前 項和,處理方法是把式子中的
項和,處理方法是把式子中的 用
用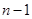 代換后,兩式相減,本題中得到
代換后,兩式相減,本題中得到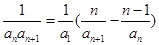 ,這個式子可整理為
,這個式子可整理為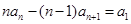 ,這是關于
,這是關于 的恒等式,因此
的恒等式,因此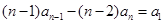
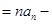
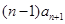 ,即
,即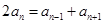 , 這就說明
, 這就說明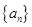 為等差數列,得證,解題時還要注意對
為等差數列,得證,解題時還要注意對 的初始值是否成立;(3)已知條件為等差數列
的初始值是否成立;(3)已知條件為等差數列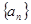 中
中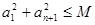 ,要求
,要求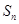 的最大值,為了能對數列
的最大值,為了能對數列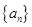 進行處理,我們利用三角換元法,對已知條件變換,設設
進行處理,我們利用三角換元法,對已知條件變換,設設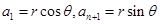 ,(
,(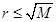 ),這樣數列的公差
),這樣數列的公差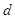 就可求出,從而也就能求出前
就可求出,從而也就能求出前 項和
項和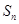 ,
,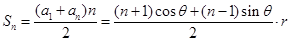 ,再利用三角函數
,再利用三角函數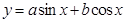 的最大值為
的最大值為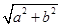 ,就能求出
,就能求出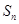 的最大值.
的最大值.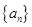 的公差為
的公差為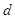 ,則原等式可化為
,則原等式可化為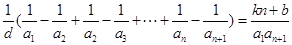 ,所以
,所以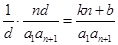 ,
,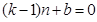 對于
對于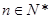 恒成立,所以
恒成立,所以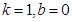 . 4分
. 4分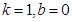 時,假設
時,假設 為
為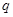 的必要條件,即“若
的必要條件,即“若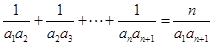 ①對于任意的
①對于任意的 (
(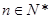 )恒成立,則
)恒成立,則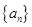 為等差數列”,
為等差數列”,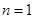 時,
時,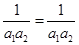 顯然成立, 6分
顯然成立, 6分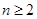 時,
時,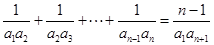 ②,由①-②得:
②,由①-②得: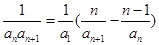 ,
,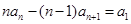 ③,
③,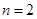 時,
時,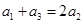 ,即
,即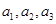 成等差數列,
成等差數列,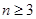 時,
時,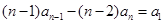 ④,由③④得
④,由③④得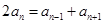 ,所以
,所以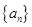 為等差數列,即
為等差數列,即 是
是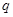 的必要條件. 10分
的必要條件. 10分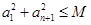 ,可設
,可設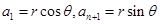 ,所以
,所以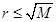 .
.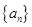 的公差為
的公差為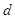 ,則
,則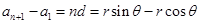 ,所以
,所以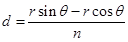 ,
,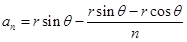 ,
,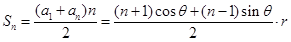
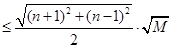
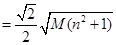 ,
,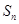 的最大值為
的最大值為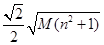 . 16分
. 16分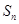 的最大值問題.
的最大值問題.

湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com