【題目】設直線
與拋物線
相交于不同兩點
、
，與圓
相切于點
，且
為線段
中點．
(1) 若
是正三角形（
是坐標原點），求此三角形的邊長；
(2) 若
，求直線
的方程；
(3) 試對
進行討論，請你寫出符合條件的直線
的條數（直接寫出結論）．
階梯計算系列答案科目：高中數學 來源： 題型：
【題目】已知動圓
與圓
： 
相切，且與圓
： 
相內切，記圓心
的軌跡為曲線
.設
為曲線
上的一個不在
軸上的動點， 
為坐標原點，過點
作
的平行線交曲線
于
, 
兩個不同的點.
（Ⅰ）求曲線
的方程；
（Ⅱ）試探究
和
的比值能否為一個常數？若能，求出這個常數，若不能，請說明理由；
（Ⅲ）記
的面積為
， 
的面積為
，令
，求
的最大值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在平面直角坐標系
中，已知以
為圓心的圓的方程為： 
，以
為圓心的圓的方程為： 
．
（1）若過點
的直線
沿
軸向左平移3個單位，沿
軸向下平移4個單位后，回到原來的位置，求直線
被圓
截得的弦長；
（2）圓
是以1為半徑，圓心在圓
： 
上移動的動圓 ，若圓
上任意一點
分別作圓
的兩條切線
，切點為
，求
的取值范圍
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知△OAB的頂點坐標為O（0，0），A（2，9），B（6，﹣3），點P的橫坐標為14，且 
，點Q是邊AB上一點，且 
．
（1）求實數λ的值與點P的坐標；
（2）求點Q的坐標；
（3）若R為線段OQ上的一個動點，試求 
的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
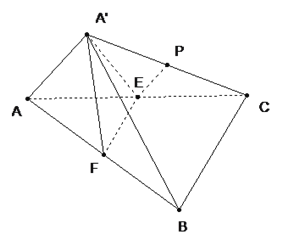
【題目】如圖， 
、
分別為直角三角形
的直角邊
和斜邊
的中點，沿
將
折起到
的位置，連結
、
， 
為
的中點．
（1）求證： 
平面
；（2）求證：平面
平面
；
（3）求證： 
平面
．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設函數
的定義域是
，對于以下四個命題：
(1) 若
是奇函數，則
也是奇函數；
(2) 若
是周期函數，則
也是周期函數；
(3) 若
是單調遞減函數，則
也是單調遞減函數；
(4) 若函數
存在反函數
，且函數
有零點，則函數
也有零點．
其中正確的命題共有
A. 1個 B. 2個 C. 3個 D. 4個
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知數列{an}，{bn}滿足a1=1，an+1=2an+1，b1=4，bn﹣bn﹣1=an+1（n≥2）．
（1）求證：數列{an+1}是等比數列；
（2）求數列{an}，{bn}的通項公式．
查看答案和解析>>
科目：高中數學 來源： 題型：
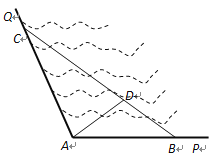
【題目】如圖所示， 
是某海灣旅游區的一角，其中
，為了營造更加優美的旅游環境，旅游區管委會決定在直線海岸
和
上分別修建觀光長廊
和AC，其中
是寬長廊，造價是
元/米， 
是窄長廊，造價是
元/米，兩段長廊的總造價為120萬元，同時在線段
上靠近點
的三等分點
處建一個觀光平臺，并建水上直線通道
（平臺大小忽略不計），水上通道的造價是
元/米．
(1) 若規劃在三角形
區域內開發水上游樂項目，要求
的面積最大，那么
和
的長度分別為多少米？
(2) 在(1)的條件下，建直線通道
還需要多少錢？
查看答案和解析>>
科目：高中數學 來源： 題型：
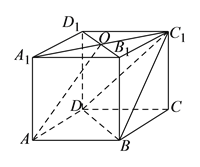
【題目】在四棱柱
中，
底面
，底面為菱形，
為
與
交點，已知
，
．
（I）求證：
平面
．
（II）在線段上是否存在一點
，使得
平面
，如果存在，求
的值，如果不存在，請說明理由．
（III）設點
在
內（含邊界），且
，求所有滿足條件的點構成的圖形，并求
的最小值．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
