
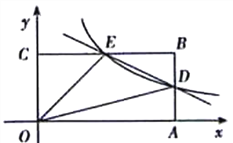
【題目】如圖,在平面直角坐標系中,原點O是矩形OABC的一個頂點,點A、C都
在坐標軸上,點B的坐標是(4.2),反比例函數![]() 與AB,BC分別交于點D,E。
與AB,BC分別交于點D,E。
(1)求直線DE的解析式;
(2)若點F為y軸上一點,△OEF和△ODE的面積相等,求點F的坐標。
【答案】(1)![]() . (2)F的坐標為(0,3)或(0,-3).
. (2)F的坐標為(0,3)或(0,-3).
【解析】試題分析:(1)先求出D、E的坐標,然后用待定系數法即可求出直線的解析式;
(2)先求出△ODE的面積,然后由△OEF和△ODE的面積相等,求出OF的長,即可得到結論.
試題解析:解:(1)由B(4,2)知,點D的橫坐標是4,點E的縱坐標是2,
又∵點D,E都在![]() 的圖象上,∴D(4,1),E(2,2).
的圖象上,∴D(4,1),E(2,2).
設直線DE的解析式為![]() ,把D(4,1),E(2,2)代入,得:
,把D(4,1),E(2,2)代入,得:
![]() 解得:
解得: 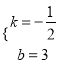
∴直線DE的解析式為![]() .
.
(2)∵D(4,1),E(2,2),B(4,2),
∴S△ODE= S矩形OABC - S△OCE - S△BDE- S△OAD![]() =3.
=3.
∵點F為y軸上一點,S△OEF=S△ODE,
∴S△OEF![]() .
.
∴OF=3.
∴F的坐標為(0,3)或(0,-3).


 口算題卡加應用題集訓系列答案
口算題卡加應用題集訓系列答案 綜合自測系列答案
綜合自測系列答案科目:初中數學 來源: 題型:
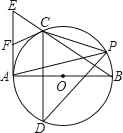
【題目】如圖,Rt△ABE中,AB⊥AE以AB為直徑作⊙O,交BE于C,弦CD⊥AB,F為AE上一點,連FC,則FC=FE
(1)求證:CF是⊙O的切線;
(2)已知點P為⊙O上一點,且tan∠APD=![]() ,連CP,求sin∠CPD的值.
,連CP,求sin∠CPD的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某公司計劃從兩家皮具生產能力相近的制造廠選擇一家來承擔外銷業務,這兩家廠生產的皮具款式和材料都符合要求,因此只需要檢測皮具質量的克數是否穩定,現從兩家提供的樣品中各抽取了6件進行檢查,超過標準質量部分記為正數,不足部分記為負數,若該皮具的標準質量為500克,測得它們質量如下(單位:g)
廠家 | 超過標準質量的部分 | |||||
甲 | ﹣3 | 0 | 0 | 1 | 2 | 0 |
乙 | ﹣2 | 1 | ﹣1 | 0 | 1 | 1 |
(1)分別計算甲、乙兩廠抽樣檢測的皮具總質量各是多少克?
(2)通過計算,你認為哪一家生產皮具的質量比較穩定?
查看答案和解析>>
科目:初中數學 來源: 題型:
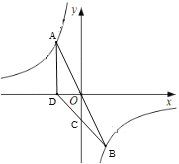
【題目】如圖,直線y=mx與雙曲線y=![]() 交于A、B兩點,D為x軸上一點,連接BD交y軸與點C,若C(0,-2)恰好為BD中點,且△ABD的面積為6,則B點坐標為__________.
交于A、B兩點,D為x軸上一點,連接BD交y軸與點C,若C(0,-2)恰好為BD中點,且△ABD的面積為6,則B點坐標為__________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某中學為了了解八年級學生的業余愛好,抽查了部分學生,并制如下表格和條形統計圖:
頻數 | 頻率 | |
體育 | 25 | 0.25 |
美術 | 30 | a |
音樂 | b | 0.35 |
其他 | 10 | 0.1 |

請根據圖完成下面題目:
(1)抽查人數為_____人,a=_____.
(2)請補全條形統計圖;
(3)若該校八年級有800人,請你估算該校八年級業余愛好音樂的學生約有多少人?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某新店開業宣傳,進店有禮活動,店員們需準備制作圓柱體禮品紙盒(如圖①),每個紙盒由1個長方形側面和2個圓形底面組成,現有100張正方形紙板全部以A或者B方法截剪制作(如圖②),設截剪時x張用A方法.
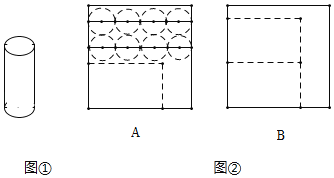
(1)根據題意,完成以下表格:
裁剪法A | 裁剪法B | |
長方形側面 | x |
|
圓形底面 |
| 0 |
(2)若裁剪出的長方形側面和圓形底面恰好用完,問能做多少個紙盒?
(3)按以上制作方法,若店員們希望準備300個禮盒,那至少還需要正方形紙板 張.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,從熱氣球C處測得地面A、B兩點的俯角分別為30°、45°,如果此時熱氣球C處的
高度CD為100m,點A、D、B在同一直線上,CD⊥AB,則A、B兩點的距離是( )

A. 200m B. 200![]() m C.
m C. ![]() m D.
m D. ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某文具店用1050元購進第一批某種鋼筆,很快賣完,又用1440元購進第二批該種鋼筆,但第二批每支鋼筆的進價是第一批進價的1.2倍,數量比第一批多了10支。
(1)求第一批每支鋼筆的進價是多少元?
(2)第二批鋼筆按24元/支的價格銷售,銷售一定數量后,根據市場情況,商店決定對剩余的鋼筆全按8折一次性打折銷售,但要求第二批鋼筆的利潤率不低于20%,問至少銷售多少支后開始打折?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(材料閱讀)數軸是數學學習的一個很重要的工具,利用數軸可以將數與形完美結合.通過數軸我們可發現許多重要的規律:
①對值的幾何意義:一般地,若點![]() 、點
、點![]() 在數軸上表示的有理數分別為
在數軸上表示的有理數分別為![]() ,
,![]() ,那么
,那么![]() 、
、![]() 兩點之間的距離表示為
兩點之間的距離表示為![]() ,記作
,記作![]() ,
,![]() 則表示數
則表示數![]() 和1在數軸上對應的兩點之間的距離;又如
和1在數軸上對應的兩點之間的距離;又如![]() ,所以
,所以![]() 表示數
表示數![]() 和
和![]() 在數軸上對應的兩點之間的距離;
在數軸上對應的兩點之間的距離;
②若數軸上點![]() 、點
、點![]() 表示的數分別為
表示的數分別為![]() 、
、![]() ,那么線段
,那么線段![]() 的中點
的中點![]() 表示的數為
表示的數為![]() .
.
(問題情境)如圖,在數軸上,點![]() 表示的數為
表示的數為![]() ,點
,點![]() 在原點右側,表示的數為
在原點右側,表示的數為![]() ,動點
,動點![]() 從點
從點![]() 出發以每秒
出發以每秒![]() 個單位長度的速度沿數軸正方向運動,同時,動點
個單位長度的速度沿數軸正方向運動,同時,動點![]() 從點
從點![]() 出發以每秒
出發以每秒![]() 個單位長度的速度沿數軸負方向運動,其中線段
個單位長度的速度沿數軸負方向運動,其中線段![]() 的中點記作點
的中點記作點![]() .
.
![]()
(綜合運用)
(1)出發![]() 秒后,點
秒后,點![]() 和點
和點![]() 相遇,則
相遇,則![]() 表示的數
表示的數![]() ___________;
___________;
(2)在第(1)問的基礎上,當![]() 時,求運動時間;
時,求運動時間;
(3)在第(1)問的基礎上,點![]() 、
、![]() 在相遇后繼續以原來的速度在這條數軸上運動,但
在相遇后繼續以原來的速度在這條數軸上運動,但![]() 、
、![]() 兩點運動的方向相同.隨著點
兩點運動的方向相同.隨著點![]() 、
、![]() 的運動,線段
的運動,線段![]() 的中點
的中點![]() 也相應移動,問線段
也相應移動,問線段![]() 的中點
的中點![]() 能否與表示
能否與表示![]() 的點重合?若能,求出從
的點重合?若能,求出從![]() 、
、![]() 相遇起經過的運動時間;若不能,請說明理由.
相遇起經過的運動時間;若不能,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com