
【題目】圖1是某浴室花灑實景圖,圖2是該花灑的側面示意圖.已知活動調節點B可以上下調整高度,離地面CD的距離BC=160cm.設花灑臂與墻面的夾角為α,可以扭動花灑臂調整角度,且花灑臂長AB=30cm.假設水柱AE垂直AB直線噴射,小華在離墻面距離CD=120cm處淋浴.

(1)當α=30°時,水柱正好落在小華的頭頂上,求小華的身高DE.
(2)如果小華要洗腳,需要調整水柱AE,使點E與點D重合,調整的方式有兩種:
①其他條件不變,只要把活動調節點B向下移動即可,移動的距離BF與小華的身高DE有什么數量關系?直接寫出你的結論;
②活動調節點B不動,只要調整α的大小,在圖3中,試求α的度數.
(參考數據:![]() ≈1.73,sin8.6°≈0.15,sin36.9°≈0.60,tan36.9°≈0.75)
≈1.73,sin8.6°≈0.15,sin36.9°≈0.60,tan36.9°≈0.75)
【答案】(1)125.4cm;(2)①BF=DE;②61.7°.
【解析】
(1)過點A作AG⊥CB的延長線于點G,交DE的延長線于點H,利用含30度角的直角三角形的性質即可求出答案.
(2)①由平行四邊形的判定與性質即可知道BF=DE;
②由勾股定理可求出BD的長度,然后根據銳角三角函數的定義可求出∠1與∠2的度數,從而可求出α的度數.
解:(1)如圖,過點A作AG⊥CB的延長線于點G,交DE的延長線于點H,
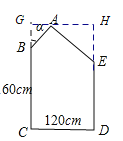
∵∠C=∠D=90°,
∴四邊形GCDH為矩形,
∴GH=CD=120,DH=CG,∠H=90°,
在Rt△ABG中,
∠ABG=α=30°,AB=30,
∴AG=15,
∴AH=120﹣15=105,
∵AE⊥AB,
∴∠EAH=30°,
又∵∠H=90°,
∴EH=AH![]() tan30°=35
tan30°=35![]() ,
,
∴ED=HD﹣HE=160+15![]() ﹣35
﹣35![]() ≈125.4(cm)
≈125.4(cm)
(2)①BF=DE;
②如圖,連接BD
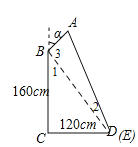
在Rt△BCD中,
BD=![]() =200,
=200,
∴sin∠1=![]() =0.6,
=0.6,
∴∠1≈36.9°,
在Rt△BAD中,AB=30.
∴sin∠2=![]() =
=![]() =0.15,
=0.15,
∴∠2≈8.6°,
∴∠3≈90°﹣8.6°=81.4°,
∴α=180°﹣∠1﹣∠3≈180°﹣36.9°﹣81.4°=61.7°.


科目:初中數學 來源: 題型:
【題目】如圖,在 Rt△ABC 中,∠ABC=90°,AB=BC,點 D 是線段 AB 上的一點,連結 CD.過點 B 作 BG⊥CD,分別交 CD、CA 于點 E、F,與過點 A 且垂直于 AB 的直線相交于點 G,連結 DF,給出以下四個結論:①![]() ;②若
;②若![]()
![]() AB,則點 D 是 AB 的中點;③若
AB,則點 D 是 AB 的中點;③若![]() ,則 S△ABC=9S△BDF;④當 B、C、F、D 四點在同一個圓上時,DF=DB;其中正確的結論序號是( )
,則 S△ABC=9S△BDF;④當 B、C、F、D 四點在同一個圓上時,DF=DB;其中正確的結論序號是( )

A.①②B.①②④C.①②③D.①②③④
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】電水壺采用的是蒸汽智能感應控溫原理,具有沸騰后自動斷電、防干燒斷電的功能.如圖1,是一電水壺的實物圖.當壺蓋打開時,壺蓋與閉合時蓋面之間的夾角可以抽象為![]() (如圖2),壺身側面與底座(壺蓋及底座厚度護理不計)之間的夾角可以抽象為
(如圖2),壺身側面與底座(壺蓋及底座厚度護理不計)之間的夾角可以抽象為![]() (如圖2)若壺嘴及手柄部分不考慮,量得壺蓋和底座的直徑分別為
(如圖2)若壺嘴及手柄部分不考慮,量得壺蓋和底座的直徑分別為![]() ,
,![]() ,
,![]() .
.
(1)求底座周長比壺蓋周長長多少?(結果保留![]() )
)
(2)若量得![]() ,求壺蓋最高點到底座所在平面的距離.
,求壺蓋最高點到底座所在平面的距離.
(結果精確到![]() ,參考數據:
,參考數據:![]() ,
,![]() ,
,![]() ,
,![]() .)
.)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知二次函數![]() ,關于此函數的圖象及性質,下列結論中不一定成立的是( )
,關于此函數的圖象及性質,下列結論中不一定成立的是( )
A.該圖象的頂點坐標為![]() B.該圖象與
B.該圖象與![]() 軸的交點為
軸的交點為![]()
C.若該圖象經過點![]() ,則一定經過點
,則一定經過點![]() D.當
D.當![]() 時,
時,![]() 隨
隨![]() 的增大而增大
的增大而增大
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,在矩形ABCD中,動點P從點B出發,沿BC﹣CD﹣DA運動至點A停止.設點P運動的路程為x,△ABP的面積為y,若y關于x的函數圖象如圖2所示,則y的最大值是( )
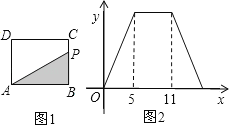
A.55B.30C.16D.15
查看答案和解析>>
科目:初中數學 來源: 題型:
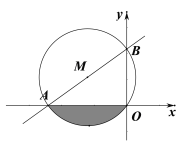
【題目】一次函數![]() 的圖像與x軸的負半軸相交于點A,與y軸的正半軸相交于點B,且
的圖像與x軸的負半軸相交于點A,與y軸的正半軸相交于點B,且![]() △OAB的外接圓的圓心M的橫坐標為-3.
△OAB的外接圓的圓心M的橫坐標為-3.
(1)求一次函數的解析式;
(2)求圖中陰影部分的面積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com