
【題目】如圖,在矩形ABCD中,AB=m(m是大于0的常數),BC=8,E為線段BC上的動點(不與B、C重合).連接DE,作EF⊥DE,EF與射線BA交于點F,設CE=x,BF=y.
(1)求y關于x的函數關系式;
(2)若m=8,求x為何值時,y的值最大,最大值是多少?
(3)若y= ![]() ,要使△DEF為等腰三角形,m的值應為多少?
,要使△DEF為等腰三角形,m的值應為多少?
【答案】
(1)
解:∵EF⊥DE,
∴∠BEF=90°-∠CED=∠CDE,
又∠B=∠C=90°,
∴△BEF∽△CDE,
∴ ![]()
即
![]()
解得y= ![]() ;
;
(2)
解:由(1)得y= ![]() ,
,
將m=8代入,得y=- ![]()
= ![]()
所以當x=4時,y取得最大值為2;
(3)
解:∵∠DEF=90°,∴只有當DE=EF時,△DEF為等腰三角形,
∴△BEF≌△CDE,
∴BE=CD=m,
此時m=8-x,解方程
![]() =
= ![]() ,
,
得x=6,或x=2,
當x=2時,m=6,
當x=6時,m=2.
【解析】本題把相似三角形與求二次函數解析式聯系起來,在解題過程中,充分運用相似三角形對應邊的比相等,建立函數關系式.(1)利用互余關系找角相等,證明△BEF∽△CDE,根據對應邊的比相等求函數關系式;(2)把m的值代入函數關系式,再求二次函數的最大值;(3)∵∠DEF=90°,只有當DE=EF時,△DEF為等腰三角形,把條件代入即可.
【考點精析】本題主要考查了二次函數的性質的相關知識點,需要掌握增減性:當a>0時,對稱軸左邊,y隨x增大而減小;對稱軸右邊,y隨x增大而增大;當a<0時,對稱軸左邊,y隨x增大而增大;對稱軸右邊,y隨x增大而減小才能正確解答此題.


 高中必刷題系列答案
高中必刷題系列答案科目:初中數學 來源: 題型:
【題目】如圖,在Rt△ABC中,∠C=90°,AC=6,BC=8,點F在邊AC上,并且CF=2,點E為邊BC上的動點,將△CEF沿直線EF翻折,點C落在點P處,則點P到邊AB距離的最小值是 . 
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某公司在![]() 兩倉庫分別有機器16臺和12臺,現要運往甲、乙兩地,其中甲地需要15臺,乙地需要13臺,已知
兩倉庫分別有機器16臺和12臺,現要運往甲、乙兩地,其中甲地需要15臺,乙地需要13臺,已知![]() 兩地倉庫運往甲,乙兩地機器的費用如下面的左表所示.
兩地倉庫運往甲,乙兩地機器的費用如下面的左表所示.
![]() 設從A倉庫調x臺機器去甲地,請用含x的代數式補全下面的右表;
設從A倉庫調x臺機器去甲地,請用含x的代數式補全下面的右表;
機器調運費用表機器調運方案表
出發地 目的地運費 | A | B | 出發地 目的地機器 | A | B | 合計 | |
甲 | 500 | 300 | 甲地 | x | 15 | ||
乙 | 400 | 600 | 乙地 | 13 | |||
合計 | 16 | 12 | 28 |
![]() 設總運費為y元,求y與x之間的函數解析式,并寫出自變量x的取值范圍;
設總運費為y元,求y與x之間的函數解析式,并寫出自變量x的取值范圍;
![]() 由機器調運方案表可知共有n種調運方案,求n的值.
由機器調運方案表可知共有n種調運方案,求n的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在![]() 中,
中, ![]() ,
, ![]() ,點
,點![]() 在
在![]() 的延長線上,
的延長線上, ![]() 是
是![]() 的中點,
的中點, ![]() 是射線
是射線![]() 上一動點,且
上一動點,且![]() ,連接
,連接![]() ,作
,作![]() ,
, ![]() 交
交![]() 延長線于點
延長線于點![]() .
.
(![]() )如圖
)如圖![]() ,當點
,當點![]() 在
在![]() 上時,填空:
上時,填空: ![]() __________
__________ ![]() (填“
(填“![]() ”、“
”、“![]() ”或“
”或“![]() ”).
”).
(![]() )如圖
)如圖![]() ,當點
,當點![]() 在
在![]() 的延長線上時,請根據題意將圖形補全,判斷
的延長線上時,請根據題意將圖形補全,判斷![]() 與
與![]() 的數量關系,并證明你的結論.
的數量關系,并證明你的結論.


查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為加強中小學生安全和禁毒教育,某校組織了“防溺水、交通安全、禁毒”知識競賽,為獎勵在競賽中表現優異的班級,學校準備從體育用品商場一次性購買若干個足球和籃球(每個足球的價格相同,每個籃球的價格相同),購買1個足球和1個籃球共需159元;足球單價是籃球單價的2倍少9元.
(1)求足球和籃球的單價各是多少元?
(2)根據學校實際情況,需一次性購買足球和籃球共20個,但要求購買足球和籃球的總費用不超過1550元,學校最多可以購買多少個足球?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如果一個實際問題的函數圖象的形狀與y= ![]() 的形狀相同,且頂點坐標是(4,-2),那么它的函數解析式為( ).
的形狀相同,且頂點坐標是(4,-2),那么它的函數解析式為( ).
A.y= ![]()
B.y= ![]() 或y=
或y= ![]()
C.y= ![]()
D.y= ![]() 或y=
或y= ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】杭州休博會期間,嘉年華游樂場投資150萬元引進一項大型游樂設施.若不計維修保養費用,預計開放后每月可創收33萬元.而該游樂設施開放后,從第1個月到第x個月的維修保養費用累計為y(萬元),且y=ax2+bx;若將創收扣除投資和維修保養費用稱為游樂場的純收益g(萬元),g也是關于x的二次函數;
(1)若維修保養費用第1個月為2萬元,第2個月為4萬元.求y關于x的解析式;
(2)求純收益g關于x的解析式;
(3)問設施開放幾個月后,游樂場的純收益達到最大;幾個月后,能收回投資?
查看答案和解析>>
科目:初中數學 來源: 題型:
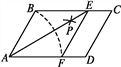
【題目】如圖,在ABCD中,以點A為圓心,AB長為半徑畫弧交AD于點F,再分別以點B,F為圓心,大于BF的相同長為半徑畫弧,兩弧交于點P;連接AP并延長交BC于點E,連接EF,則所得四邊形ABEF是菱形.
(1)根據以上尺規作圖的過程,求證:四邊形ABEF是菱形;
(2)若菱形ABEF的周長為16,AE=![]() ,求∠C的大小.
,求∠C的大小.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】點P(x,y)在第一象限內,且x+y=6,點A的坐標為(4,0).設△OPA的面積為S,則下列圖象中,能正確反映面積S與x之間的函數關系式的圖象是( )
A.
B.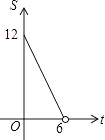
C.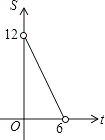
D.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com