
【題目】今年4月,我市某中學舉行了“愛我中國朗誦比賽”活動,根據學生的成績劃分為A、B、C、D四個等級,并繪制了如下兩種不完整的統計圖.根據圖中提供的信息,回答下列問題:
(1)參加朗誦比賽的學生共有 ,并把條形統計圖補充完整;
(2)扇形統計圖中,m= ,n= ;C等級對應扇形的圓心角為 度;
(3)學校準備從獲A等級的學生中隨機選取2人,參加市舉辦的朗誦比賽,請利用列表法或樹形圖法,求獲A等級的小明參加市朗誦比賽的概率.

【答案】(1)40, (2) 10; 40; 144°;(3)![]() .
.
【解析】(1)根據D等級的有12人,占總數的30%,即可求得總人數,利用總人數減去其它等級的人數求得B等級的人數,從而作出直方圖;
(2)根據百分比的定義求得m、n的值,利用360°乘以C等級所占的百分比即可求得對應的圓心角;
(3)利用列舉法即可求A等級的小明參加市比賽的概率.
試題分析:
試題解析:解:(1)參加演講比賽的學生共有:12÷30%=40(人),
則B等級的人數是:40![]() =8(人).將條形圖補充完整如下:
=8(人).將條形圖補充完整如下:
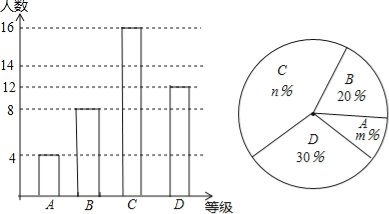
(2)A所占的比例是: ![]() ×100%=10%,∴m="10" ;
×100%=10%,∴m="10" ;
C所占的百分比: ![]() ×100%=40%.∴n=40;
×100%=40%.∴n=40;
C等級對應扇形的圓心角是:360×40%=144°;
(3)設A等級的小明用a表示,其他的幾個學生用b、c、d表示.
![]()
共有12種情況,其中小明參加的情況有6種,則P(小明參加比賽)=![]() =
=![]() .
.


科目:初中數學 來源: 題型:
【題目】如圖,在矩形ABCD中,AB=5,AD=4,E為AD邊上一動點(不與點A重合),AF⊥BE,垂足為F,GF⊥CF,交AB于點G,連接EG.設AE=x,S△BEG=y.
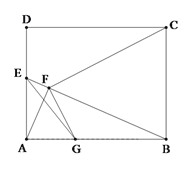
(1)證明:△AFG∽△BFC;
(2)求y與x的函數關系式,并求出y的最大值;
(3)若△BFC為等腰三角形,請直接寫出x的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列各式由左到右的變形正確的是( )
A. -x-y=-(x-y) B. -x2+2xy-y2=-(x2+2xy+y2)
C. (y-x)2=(x-y)2 D. (y-x)3=(x-y)3
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com