
【題目】拋物線y=ax2+bx+c(a≠0)如圖所示,現有下列四個結論:①abc>0 ②b2-4ac<0 ③c<4b ④a+b>0.其中正確的結論有( )

A. 1個 B. 3個 C. 2個 D. 4個
【答案】C
【解析】
根據拋物線開口方向得a<0,再根據對稱軸得b>0,根據拋物線與y軸的交點在x軸上方得c>0,于是abc<0,所以可對①進行判斷;
根據拋物線與x軸有兩個交點可對②進行判斷;
根據拋物線的對稱軸為直線x=-![]() =1,則b=-2a,拋物線與x軸另一交點坐標為(-1,0),所以當x=-2時,y<0,即4a-2b+c<0,然后把a=-
=1,則b=-2a,拋物線與x軸另一交點坐標為(-1,0),所以當x=-2時,y<0,即4a-2b+c<0,然后把a=-![]() b代入得到c<4b,于是可對③進行判斷;
b代入得到c<4b,于是可對③進行判斷;
根據b=-2a可得a+b=-a>0,則可對④進行判斷.
∵拋物線開口相下,
∴a<0,
∵拋物線對稱軸為直線x=-![]() >0,
>0,
∴b>0,
∵拋物線與y軸的交點在x軸上方,
∴c>0,
∴abc<0,所以①錯誤;
∵拋物線與x軸有兩個交點,
∴b2-4ac>0,所以②錯誤;
∵對稱軸為直線x=-![]() =1,
=1,
∴b=-2a,拋物線與x軸另一交點坐標為(-1,0),
∴當x=-2時,y<0,即4a-2b+c<0,
∴-2b-2b+c<0,即c<4b,所以③正確;
∵b=-2a,
∴a+b=-a>0,所以④正確.
故選:C


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
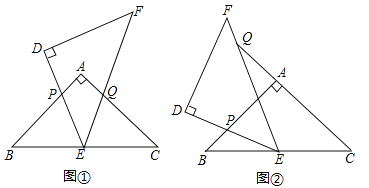
【題目】(2017甘肅省天水市)△ABC和△DEF是兩個全等的等腰直角三角形,∠BAC=∠EDF=90°,△DEF的頂點E與△ABC的斜邊BC的中點重合,將△DEF繞點E旋轉,旋轉過程中,線段DE與線段AB相交于點P,線段EF與射線CA相交于點Q.
(1)如圖①,當點Q在線段AC上,且AP=AQ時,求證:△BPE≌△CQE;
(2)如圖②,當點Q在線段CA的延長線上時,求證:△BPE∽△CEQ;并求當BP=2,CQ=9時BC的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,四邊形ABCD為平行四邊形紙片.把紙片ABCD折疊,使點B恰好落在CD邊上,折痕為AF.且AB=10cm、AD=8cm、DE=6cm.
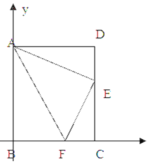
(1)求證:平行四邊形ABCD是矩形;
(2)如圖2,以點B為坐標原點,水平方向、豎直方向為x軸、y軸建立平面直角坐標系,求直線AF的解析式;
(3)在(2)中的坐標系內是否存在這樣的點P,使得以點P、A、E、F為頂點的四邊形是平行四邊形?若不存在,請說明理由;若存在,直接寫出點P的坐標。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】古希臘著名的畢達哥拉斯學派把1,3,6,10…這樣的數稱為“三角形數”,而把1,4,9,16…這樣的數稱為“正方形數”.從圖中可以發現,任何一個大于1的“正方形數”都可以看作兩個相鄰“三角形數”之和.下列等式中,符合這一規律的是( )
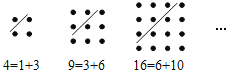
A.13=3+10B.25=9+16C.36=15+21D.49=18+31
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知![]() 是關于
是關于![]() 的方程
的方程![]() 的一個實數根,并且這個方程的兩個實數根恰好是等腰三角形
的一個實數根,并且這個方程的兩個實數根恰好是等腰三角形![]() 的兩條邊長,則
的兩條邊長,則![]() 的周長為( )
的周長為( )
A. 6 B. 8 C. 10 D. 8或10
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點A是一次函數y=﹣![]() x+
x+![]() 的圖象與反比例函數y=
的圖象與反比例函數y=![]() (m>0)的圖象的一個交點,AB⊥x軸,垂足為B,且AB=
(m>0)的圖象的一個交點,AB⊥x軸,垂足為B,且AB=![]() .
.
(1)求這個反比例函數的解析式;
(2)當1<x<4,求反比例函數y=![]() 的取值范圍.
的取值范圍.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某商場銷售兩種型號的飲水機,八月份銷售A種型號的飲水機150個和B種型號的飲水機200個.
(1)商場八月份銷售飲水機時,A種型號的售價比B種型號的2倍少10元,總銷售額為88500元,那么B種型號的飲水機的單價是每件多少元?
(2)為了提高銷售量,商場九月份銷售飲水機時,A種型號的售價比八月份A種型號售價下降了![]() a%(a>0),且A種型號的銷量比八月份A種型號的銷量提高了a%;B種型號的售價比八月份的B種型號的售價下降了a%,但B種型號的銷售量與八月份的銷售量相同,結果九月份的總銷售額也是88500元,求a的值.
a%(a>0),且A種型號的銷量比八月份A種型號的銷量提高了a%;B種型號的售價比八月份的B種型號的售價下降了a%,但B種型號的銷售量與八月份的銷售量相同,結果九月份的總銷售額也是88500元,求a的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為準備母親節禮物,同學們委托小明用其支付寶余額團購鮮花或禮盒.每束鮮花的售價相同,每份禮盒的售價也相同.若團購15束鮮花和18份禮盒,余額差80元;若團購18束鮮花和15份禮盒,余額剩70元.若團購19束鮮花和14份禮盒,則支付寶余額剩_______元.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com