
【題目】△ABC中,∠C=90°,∠A=60°,AC=2cm.長為1cm的線段MN在△ABC的邊AB上沿AB方向
以1cm/s的速度向點B運動(運動前點M與點A重合).過M,N分別作AB的垂線交直角邊于P,Q兩點,線段MN運動的時間為ts.
(1)若△AMP的面積為y,寫出y與t的函數關系式(寫出自變量t的取值范圍);
(2)線段MN運動過程中,四邊形MNQP有可能成為矩形嗎?若有可能,求出此時t的值;若不可能,說明理由;
(3)t為何值時,以C,P,Q為頂點的三角形與△ABC相似?

【答案】(1)y與t的函數關系式為
(2)當![]() 時,四邊形MNQP為矩形 ;
時,四邊形MNQP為矩形 ;
(3)當![]() 或
或![]() 時,以C,P,Q為頂點的三角形與△ABC相似.
時,以C,P,Q為頂點的三角形與△ABC相似.
【解析】試題分析:(1)分兩種情況,點P可以在AC上時和當點P在BC上時,利用三角函數分別用含t的代數式表示出PM,AM,再用S△APM=![]() AMPM得出y與t的函數關系式,(2)當PM=QN時,四邊形MNQP為矩形,建立含t的方程,求得t的值,(3)以C,P,Q為頂點的三角形與△ABC相似有兩種情況,△PQC∽△ABC時和△QPC∽△ABC,分別相似三角形的判定和性質,求得相對應的t的值.
AMPM得出y與t的函數關系式,(2)當PM=QN時,四邊形MNQP為矩形,建立含t的方程,求得t的值,(3)以C,P,Q為頂點的三角形與△ABC相似有兩種情況,△PQC∽△ABC時和△QPC∽△ABC,分別相似三角形的判定和性質,求得相對應的t的值.
試題解析:(1)當點P在AC上時,
∵AM=t ,
![]()
![]()
當點P在BC上時,
![]()
![]()
(2)∵AC=2,∴AB=4,∴BN=AB-AM-MN=4-t=3-t
![]()
由條件可知,若四邊形MNQP為矩形,需PM=QN,
![]()
![]()
![]() ,
,
![]()
∴△PQC∽△ABC,
除此之外,當∠CPQ=∠B=30°時,△QPC∽△△ABC,
![]() ,
,
![]()
∴AP=2AM=2t,
∴CP=2-2t,
![]() ,
,
 ,
,
![]()
![]()

![]()


科目:初中數學 來源: 題型:
【題目】已知:如圖,在△ABC中,M是邊AB的中點,D是邊BC延長線上的一點,且CD= ![]() BC,作DN∥CM交AC于點N.求證:四邊形MCDN是平行四邊形.
BC,作DN∥CM交AC于點N.求證:四邊形MCDN是平行四邊形. 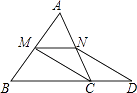
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】兩條直線被第三條直線所截,若∠1與∠2 是同旁內角,且∠1=70,則 ( )
A. ∠2=70B. ∠2=110
C. ∠2=70或∠2=110D. ∠2的度數不能確定
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,正方形ABCD的邊AB在數軸上,數軸上點A表示的數為-1,正方形ABCD的面積為16.
(1)數軸上點B表示的數為 ;
(2)將正方形ABCD沿數軸水平移動,移動后的正方形記為![]() ,移動后的正方形
,移動后的正方形![]() 與原正方形ABCD重疊部分的面積記為S.
與原正方形ABCD重疊部分的面積記為S.
① 當S =4時,畫出圖形,并求出數軸上點![]() 表示的數;
表示的數;
② 設正方形ABCD的移動速度為每秒2個單位長度,點E為線段![]() 的中點,點F在線段
的中點,點F在線段![]() 上,且
上,且![]() . 經過
. 經過![]() 秒后,點E,F所表示的數互為相反數,直接寫出
秒后,點E,F所表示的數互為相反數,直接寫出![]() 的值.
的值.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知C,D,E三點在直線AB上,P為直線AB外一點,PC=1,PD=2,PE=3,則點P到直線AB的距離( )
A. 小于1B. 不小于1C. 大于1D. 不大于1
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知BD是矩形ABCD的對角線. 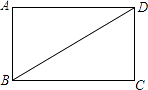
(1)用直尺和圓規作線段BD的垂直平分線,分別交AD、BC于E、F(保留作圖痕跡,不寫作法和證明).
(2)連結BE,DF,問四邊形BEDF是什么四邊形?請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某班體育課上,老師測試10個同學做引體向上的成績,10個同學的成績記錄見下表:
引體向上的個數 | 5 | 6 | 7 |
人數 | 3 | 4 | 3 |
則這10個同學做引體向上的成績的平均數是( )
A. 4 B. 5 C. 6 D. 7
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,OE是∠AOD的平分線,OC是∠BOD的平分線.
(1)若∠AOB=130°,則∠COE是多少度?
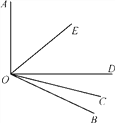
(2)在(1)的條件下,若∠COD=20°,則∠BOE是多少度?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com