
【題目】若一數軸上存在兩動點,當第一次相遇后,速度都變為原來的兩倍,第二次相遇后又都能恢復到原來的速度,則稱這條數軸為魔幻數軸.
如圖,已知一魔幻數軸上有A,O,B三點,其中A,O對應的數分別為﹣10,0,AB為47個單位長度,甲,乙分別從A,O兩點同時出發,沿數軸正方向同向而行,甲的速度為3個單位/秒,乙的速度為1個單位/秒,甲到達點B后以當時速度立即返回,當甲回到點A時,甲、乙同時停止運動.
![]()
問:(1)點B對應的數為 ,甲出發 秒后追上乙(即第一次相遇)
(2)當甲到達點B立即返回后第二次與乙相遇,求出相遇點在數軸上表示的數是多少?
(3)甲、乙同時出發多少秒后,二者相距2個單位長度?(請直接寫出答案)
【答案】(1)點B對應的數為37,甲出發5秒后追上乙(即第一次相遇);(2)相遇點在數軸上表示的數是21;(3)甲、乙同時出發4秒或5.5秒或12.75秒或13.5秒后,二者相距2個單位長度.
【解析】
(1)根據兩點間的距離可求點B對應的數,可設甲出發x秒后追上乙(即第一次相遇),根據速度差×時間=路程差,列出方程求解即可;
(2)先求出第二次與乙相遇需要的時間,進一步可求相遇點在數軸上表示的數;
(3)分第一次相遇前后相距2個單位長度,第二次相遇前后相距2個單位長度,進行討論即可求解.
解:(1)點B對應的數為:﹣10+47=37,
設甲出發x秒后追上乙(即第一次相遇),依題意有:
(3﹣1)x=10,
解得:x=5.
故甲出發5秒后追上乙(即第一次相遇);
(2)﹣10+5×3=﹣10+15=5,
37﹣5=32,
32×2÷(3×2+1×2)=8(秒),
5+1×2×8=21.
故相遇點在數軸上表示的數是:21;
(3)第一次相遇前后相距2個單位長度,
5﹣2÷(3﹣1)=5﹣1=4(秒)
5+2÷(3×2﹣1×2)=5+0.5=5.5(秒)
第二次相遇前后相距2個單位長度,
5+8﹣2÷(3×2+1×2)=12.75(秒)
5+8+2÷(3+1)=13.5(秒)
故甲、乙同時出發4秒或5.5秒或12.75秒或13.5秒后,二者相距2個單位長度.


科目:初中數學 來源: 題型:
【題目】已知在數軸上,一動點![]() 從原點
從原點![]() 出發,沿直線以每秒鐘
出發,沿直線以每秒鐘![]() 個單位長度的速度來回移動,其移動方式是先向右移動
個單位長度的速度來回移動,其移動方式是先向右移動![]() 個單位長度,再向左移動
個單位長度,再向左移動![]() 個單位長度,又向右移動
個單位長度,又向右移動![]() 個單位長度,再向左移動
個單位長度,再向左移動![]() 個單位長度,又向右移動
個單位長度,又向右移動![]() 個單位長度…
個單位長度…
![]()
(1)求出![]() 秒鐘后動點
秒鐘后動點![]() 所處的位置;
所處的位置;
(2)如果在數軸上還有一個定點![]() ,且
,且![]() 與原點
與原點![]() 相距20個單位長度,問:動點
相距20個單位長度,問:動點![]() 從原點出發,可能與點
從原點出發,可能與點![]() 重合嗎?若能,則第一次與點
重合嗎?若能,則第一次與點![]() 重合需多長時間?若不能,請說明理由.
重合需多長時間?若不能,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖①,在四邊形ABCD的邊AB上任取一點E(點E不與A,B重合),分別連接ED,EC,可以把四邊形ABCD分成三個三角形,如果其中有兩個三角形相似,我們就把E叫做四邊形ABCD的邊AB上的“相似點”;如果這三個三角形都相似,我們就把E叫做四邊形ABCD的邊AB上的“強相似點”.
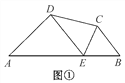
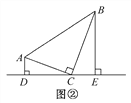
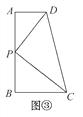
【試題再現】如圖②,在△ABC中,∠ACB=90°,直角頂點C在直線DE上,分別過點A,B作AD⊥DE于點D,BE⊥DE于點E.求證:△ADC∽△CEB.
【問題探究】在圖①中,若∠A=∠B=∠DEC=40°,試判斷點E是否是四邊形ABCD的邊AB上的相似點,并說明理由.
【深入探究】如圖③,AD∥BC,DP平分∠ADC,CP平分∠BCD交DP于點P,過點P作AB⊥AD于點A,交BC于點B.
(1)請證明點P是四邊形ABCD的邊AB上的一個強相似點.
(2)若AD=3,BC=5,試求AB的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
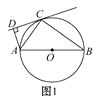
【題目】如圖1,AB是☉O的直徑,C為☉O上一點,直線CD與☉O相切于點C,AD⊥CD,垂足為D.
(1)求證:△ACD∽△ABC.
(2)如圖2,將直線CD向下平移與☉O相交于點C,G,但其他條件不變.若AG=4,BG=3,求tan∠CAD的值.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】王先生到泉州臺商投資區行政服務中心大樓辦事,假定乘電梯向上一樓記作+1,向下一樓記作﹣1,王先生從1樓出發,電梯上下樓層依次記錄如下:(單位:層)
+6,﹣3,+10,﹣8,+12,﹣7,﹣10.
(1)請你通過計算說明王先生最后是否回到出發點1樓.
(2)該中心大樓每層高3m,電梯每向上或下1m需要耗電0.1度,根據王先生現在所處位置,請你算算,他辦事時電梯需要耗電多少度?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平行四邊形ABCD中,AB=6cm,BC=12cm.∠B=30°.點P在BC上由點B向點C出發,速度為每秒2cm;點Q在邊AD上,同時由點D向點A運動,速度為每秒1cm,當點P運動到點C時,P、Q同時停止運動.連接PQ,設運動時間為t秒.
(1)當t為何值時四邊形ABPQ為平行四邊形?
(2)設四邊形ABPQ的面積為y,求y與t之間的函數關系式.
(3)當t為何值時,四邊形ABPQ的面積是四邊形ABCD的面積的四分之三,并求出此時∠PQD的度數.
(4)連結AP,是否存在某一時刻t,使△ABP為等腰三角形?并求出此刻t的值.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,已知△ABC中,AB=BC=1,∠ABC=90°,把一塊含30°角的直角三角板DEF的直角頂點D放在AC的中點上(直角三角板的短直角邊為DE,長直角邊為DF),將直角三角板DEF繞D點按逆時針方向旋轉.
(1)在圖1中,DE交AB于M,DF交BC于N.
①求證:DM=DN;
②在這一旋轉過程中,直角三角板DEF與△ABC的重疊部分為四邊形DMBN,請說明四邊形DMBN的面積是否發生變化?若發生變化,請說明是如何變化的?若不發生變化,求出其面積;
(2)繼續旋轉至如圖2的位置,延長AB交DE于M,延長BC交DF于N,DM=DN是否仍然成立?若成立,請給出證明;若不成立,請說明理由;
(3)繼續旋轉至如圖3的位置,延長FD交BC于N,延長ED交AB于M,DM=DN是否仍然成立?請寫出結論,不用證明.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某市教育局為了了解初二學生每學期參加綜合實踐活動的情況,隨機抽樣調查了某校初二學生一個學期參加綜合實踐活動的天數,并用得到的數據繪制了下面兩幅不完整的統計圖.請你根據圖中提供的信息,回答下列問題:

(1)扇形統計圖中a的值為 ;
(2)補全頻數分布直方圖;
(3)在這次抽樣調查中,眾數是 天,中位數是 天;
(4)請你估計該市初二學生每學期參加綜合實踐活動的平均天數約是多少?(結果保留整數)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com