
【題目】已知:如圖,在平行四邊形ABDC中,∠ABC的平分線交AD于點E,過點A作BE的垂線交BE于點F,交BC于點G,連接EG,CF.
(1)求證:四邊形AEGE是菱形;
(2)若∠ABC=60°,AB=4,AD=5,求CF的長.
【答案】
(1)
證明:∵BE平分∠ABC,
∴∠ABE=∠CBE,
∵四邊形ABCD是平行四邊形
∴AD∥BC且AD=BC,
∴∠CBE=∠AEB,
∴∠ABE=∠AEB=∠CBE,∴AB=AE,
∵AF⊥BE,
∴∠AFB=∠GFB=90°,
在△ABF和△GBF中,  ,
,
∴△ABF≌△GBF(ASA),
∴AB=GB,
∴AE=GB,
又∵AD∥BC,
∴四邊形ABGE是平行四邊形,
又∵AB=GB,
∴四邊形ABGE是菱形;
(2)
解:過點F作FM⊥BC于點M,如圖所示:

∵四邊形ABGE是菱形,
∴∠GBE= ![]() ∠ABC=30°,BG=AB=4,BC=AD=5,
∠ABC=30°,BG=AB=4,BC=AD=5,
在Rt△BFG中,BF=cos∠GBF×BG=cos30°×4= ![]() ×4=2
×4=2 ![]() ,
,
在Rt△BFM中,FM= ![]() BF=
BF= ![]() ×2
×2 ![]() =
= ![]() ,
,
BM=cos∠GBF×BF=cos30°×BF= ![]() ×2
×2 ![]() =3,
=3,
∴CM=BC﹣BM=5﹣3=2,
∴Rt△FMC中,CF= ![]() =
= ![]() =
= ![]() .
.
【解析】(1)先證明AB=AE,由ASA證明△ABF≌△GBF,得出AB=GB,因此AE=GB,證出四邊形ABGE是平行四邊形,即可得出結論;(2)過點F作FM⊥BC于點M,由菱形的性質得出∠GBE= ![]() ∠ABC=30°,BG=AB=4,BC=AD=5,在Rt△BFG中,由三角函數求出BF=2
∠ABC=30°,BG=AB=4,BC=AD=5,在Rt△BFG中,由三角函數求出BF=2 ![]() ,在Rt△BFM中,求出FM=
,在Rt△BFM中,求出FM= ![]() ,再求出BM=3,得出CM=BC﹣BM=5﹣3=2,Rt△FMC中,由勾股定理即可得出CF的長.
,再求出BM=3,得出CM=BC﹣BM=5﹣3=2,Rt△FMC中,由勾股定理即可得出CF的長.
【考點精析】解答此題的關鍵在于理解平行四邊形的性質的相關知識,掌握平行四邊形的對邊相等且平行;平行四邊形的對角相等,鄰角互補;平行四邊形的對角線互相平分.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
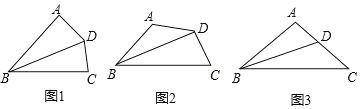
【題目】如圖,在四邊形ABCD中,∠BAD=α,∠BCD=180°﹣α,BD平分∠ABC.
(1)如圖,若α=90°,根據教材中一個重要性質直接可得 DA=CD,這個性質是__________.
(2)問題解決:如圖,求證AD=CD;
(3)問題拓展:如圖,在等腰△ABC中,∠BAC=100°,BD平分∠ABC,求證:BD+AD=BC.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,我們把橫 、縱坐標都是整數的點叫做整點.已知點
中,我們把橫 、縱坐標都是整數的點叫做整點.已知點
A(0,4),點B是![]() 軸正半軸上的整點,記△AOB內部(不包括邊界)的整點個數為m.當m=3時,點B的橫坐標的所有可能值是 ▲ ;當點B的橫坐標為4n(n為正整數)時,m= (用含n的代數式表示.)
軸正半軸上的整點,記△AOB內部(不包括邊界)的整點個數為m.當m=3時,點B的橫坐標的所有可能值是 ▲ ;當點B的橫坐標為4n(n為正整數)時,m= (用含n的代數式表示.)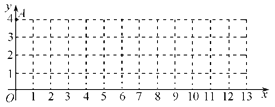
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】隨著“中國詩詞大會”節目的熱播,《唐詩宋詞精選》一書也隨之熱銷.如果一次性購買10本以上,超過10本的那部分書的價格將打折,并依此得到付款金額y(單位:元)與一次性購買該書的數量x(單位:本)之間的函數關系如圖所示,則下列結論錯誤的是( ) 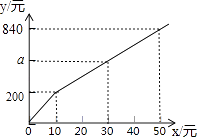
A.一次性購買數量不超過10本時,銷售價格為20元/本
B.a=520
C.一次性購買10本以上時,超過10本的那部分書的價格打八折
D.一次性購買20本比分兩次購買且每次購買10本少花80元
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系中,拋物線y=﹣ ![]() x2+bx+c與x軸交于點A(﹣4,0)、B(6,0)兩點,與y軸交于點C.
x2+bx+c與x軸交于點A(﹣4,0)、B(6,0)兩點,與y軸交于點C.
(1)如圖l,求拋物線的解析式;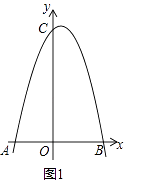
(2)如圖2,點P為第一象限拋物線上一點,連接PC、PA,PA交y軸于點F,設點P的橫坐標為t,△CPF的面積為S.求S與t的函數關系式(不要求寫出自變量t的取值范圍);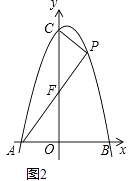
(3)如圖3,在(2)的條件下,連接BC,過點P作PD∥y軸變BC于點D,點H為AF中點,且點N(0,1),連接NH、BH,將∠NHB繞點H逆時針旋轉,使角的一條邊H落在射線HF上,另一條邊HN變拋物線于點Q,當BH=BD時,求點Q坐標.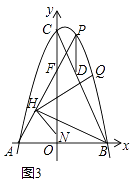
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在數軸上,點A、B分別表示點﹣5、3,M、N兩點分別從A、B同時出發以3cm/s、1cm/s的速度沿數軸向右運動.
(1)求線段AB的長;
(2)求當點M、N重合時,它們運動的時間;
(3)M、N在運動的過程中是否存在某一時刻,使BM=2BN.若存在請求出它們運動的時間,若不存在請說明理由.
![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,四邊形ABHK是邊長為6的正方形,點C、D在邊AB上,且AC=DB=1,點P是線段CD上的動點,分別以AP、PB為邊在線段AB的同側作正方形AMNP和正方形BRQP,E、F分別為MN、QR的中點,連接EF,設EF的中點為G,則當點P從點C運動到點D時,點G移動的路徑長為( )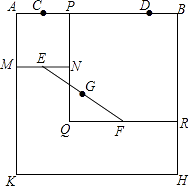
A.1
B.2
C.3
D.6
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,將邊長為3的正六邊形鐵絲框ABCDEF變形為以點A為圓心,AB為半徑的扇形(忽略鐵絲的粗細).則所得扇形AFB(陰影部分)的面積為( ) 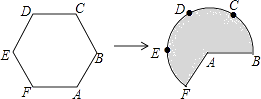
A.6π
B.18
C.18π
D.20
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com