
【題目】某校八年級數學興趣小組的同學調查了若干名家長對“初中生帶手機上學”現象的看法,統計整理并制作了如下的條形與扇形統計圖。依據圖中信息,解答下列問題:
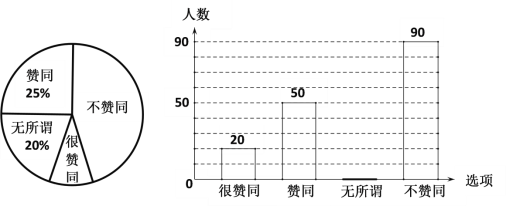
(1)接受這次調查的家長共有 人;
(2)補全條形統計圖;
(3)在扇形統計圖中,“很贊同”的家長占被調查家長總數的百分比是 ;
(4)在扇形統計圖中,“不贊同”的家長部分所對應扇形的圓心角度數是 度.
【答案】(1)200;(2)見解析;(3)10%;(4)162.
【解析】
:(1)用“贊同”的家長數除以對應的百分比就是調查的家長總人數;
(2)用調查的家長總人數乘“無所謂”的家長百分比就是“無所謂”的家長人數,由此即可補全條形統計圖;
(3)用“很贊同”的家長數除以總數即可得答案;
(4)用 “不贊同”的家長所占的比例乘360°即可.
(1)這次調查的家長總人數為:50÷25%=200(人),
故答案為:200;
(2)表示“無所謂”的家長人數為:200×20%=40(人),
補全條形統計圖如圖所示:

(3)在扇形統計圖中,“很贊同”的家長占被調查家長總數的百分比是:
![]() ×100%=10%,
×100%=10%,
故答案為:10%;
(4)“不贊同”的扇形的圓心角度數為:![]() ×360°=162°,
×360°=162°,
故答案為:162.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】如圖,數軸上有 A、B 兩點,所表示的有理數分別為 a、b,已知 AB=12,原點 O 是線段AB 上的一點,且 OA=2OB.
![]()
(1)求a,b;
(2)若動點 P,Q 分別從 A,B 同時出發,向右運動,點 P 的速度為每秒 2 個單位長度,點 Q 的速度為每秒 1 個單位長度,設運動時間為 t 秒,當點 P 與點 Q 重合時,P,Q 兩點停止運動.
①當 t 為何值時,2OPOQ=4;
②當點 P 到達點 O 時,動點 M 從點 O 出發,以每秒 3 個單位長度的速度也向右運動,當點 M 追上點 Q 后立即返回,以同樣的速度向點 P 運動,遇到點 P 后再立即返回,以同樣的速度向點 Q 運動,如此往返,直到點 P,Q 停止時,點 M 也停止運動,求在此過程中點 M 行駛的總路程,并直接寫出點 M 最后位置在數軸上所對應的有理數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC中,AB=AC,以AB為直徑作⊙O,交BC于點D,交CA的延長線于點E,連接AD、DE. 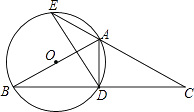
(1)求證:D是BC的中點;
(2)若DE=3,BD﹣AD=2,求⊙O的半徑;
(3)在(2)的條件下,求弦AE的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖①,在△ABC中,∠ABC與∠ACB的平分線相交于點P.
(1)如果∠A=80°,求∠BPC的度數;
(2)如圖②,作△ABC外角∠MBC,∠NCB的角平分線交于點Q,試探索∠Q、∠A之間的數量關系.
(3)如圖③,延長線段BP、QC交于點E,△BQE中,存在一個內角等于另一個內角的2倍,求∠A的度數.


查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列說法正確的是( )
A. 長方形的長是![]() 米,寬比長短25米,則它的周長可表示為
米,寬比長短25米,則它的周長可表示為![]() 米
米
B. ![]() 表示底為6,高為
表示底為6,高為![]() 的三角形的面積
的三角形的面積
C. ![]() 表示一個兩位數,它的個位數字是
表示一個兩位數,它的個位數字是![]() 十位數字是
十位數字是![]()
D. 甲、乙兩人分別從相距40千米的兩地相向出發,其行走的速度分別為3千米/小時和5千米/小時,經過![]() 小時相遇,則可列方程為
小時相遇,則可列方程為![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在Rt△ABC中,∠ACB=90°,AC=4,BC=6,點D是邊BC的中點,點E是邊AB上的任意一點(點E不與點B重合),沿DE翻折△DBE使點B落在點F處,連接AF,則線段AF的長取最小值時,BF的長為 . 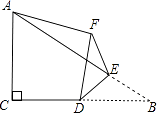
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知四邊形ABCD是平行四邊形(如圖),把△ABD沿對角線BD翻折180°得到△AˊBD.
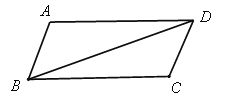
(1)利用尺規作出△AˊBD.(要求保留作圖痕跡,不寫作法);
(2)設D Aˊ 與BC交于點E,求證:△BAˊE≌△DCE.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com