
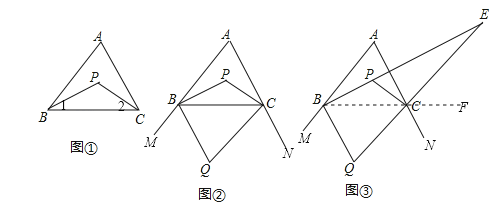
【題目】如圖①,在△ABC中,∠ABC與∠ACB的平分線相交于點P.
(1)如果∠A=80°,求∠BPC的度數;
(2)如圖②,作△ABC外角∠MBC,∠NCB的角平分線交于點Q,試探索∠Q、∠A之間的數量關系.
(3)如圖③,延長線段BP、QC交于點E,△BQE中,存在一個內角等于另一個內角的2倍,求∠A的度數.


【答案】(1)∠P=130°;(2)∠Q=90°-![]() ∠A;(3)∠A=60°、120°、90°
∠A;(3)∠A=60°、120°、90°
【解析】試題分析:(1)運用三角形的內角和定理及角平分線的定義,首先求出∠1+∠2,進而求出∠BPC即可解決問題;
(2)根據三角形的外角性質分別表示出∠MBC與∠BCN,再根據角平分線的性質可求得∠CBQ+∠BCQ,最后根據三角形內角和定理即可求解;
(3)在△BQE中,由于∠Q=90°﹣![]() ∠A,求出∠E=
∠A,求出∠E=![]() ∠A,∠EBQ=90°,所以如果△BQE中,存在一個內角等于另一個內角的2倍,那么分四種情況進行討論:①∠EBQ=2∠E=90°;②∠EBQ=2∠Q=90°;③∠Q=2∠E;④∠E=2∠Q;分別列出方程,求解即可.
∠A,∠EBQ=90°,所以如果△BQE中,存在一個內角等于另一個內角的2倍,那么分四種情況進行討論:①∠EBQ=2∠E=90°;②∠EBQ=2∠Q=90°;③∠Q=2∠E;④∠E=2∠Q;分別列出方程,求解即可.
試題解析:(1)如圖①,∵在△ABC中,∠A+∠ABC+∠ACB=180°,且∠A=80°,∴∠ABC+∠ACB=100°,∵∠1=![]() ∠ABC,∠2=
∠ABC,∠2=![]() ∠ACB,∴∠1+∠2=
∠ACB,∴∠1+∠2=![]() (∠ABC+∠ACB)=
(∠ABC+∠ACB)=![]() ×100°=50°,∴∠BPC=180°﹣(∠1+∠2)=180°﹣50°=130°.
×100°=50°,∴∠BPC=180°﹣(∠1+∠2)=180°﹣50°=130°.
(2)如圖②,∵∠MBC=∠A+∠ACB,∠BCN=∠ABC+∠A,∴∠MBC+∠BCN=∠A+∠ABC+∠ACB+∠A=180°+∠A.
∵BE,CQ分別為△ABC的外角∠MBC,∠NCB的角平分線,∴∠CBQ+∠BCQ=![]() (180°+∠A),∴∠Q=180°﹣(∠CBQ+∠BCQ)=90°﹣
(180°+∠A),∴∠Q=180°﹣(∠CBQ+∠BCQ)=90°﹣![]() ∠A;
∠A;
(3)如圖③,連結BC并延長到點F.
∵CQ為△ABC的外角∠NCB的角平分線,∴CE是△ABC的外角∠ACF的平分線,∴∠ACF=2∠ECF,∵BE平分∠ABC,∴∠ABC=2∠EBC,∵∠ECF=∠EBC+∠E,∴2∠ECF=2∠EBC+2∠E,即∠ACF=∠ABC+2∠E,又∵∠ACF=∠ABC+∠A,∴∠A=2∠E,即∠E=![]() ∠A;
∠A;
∵∠EBQ=∠EBC+∠CBQ
=![]() ∠ABC+
∠ABC+![]() ∠MBC
∠MBC
=![]() (∠ABC+∠A+∠ACB)=90°.
(∠ABC+∠A+∠ACB)=90°.
如果△BQE中,存在一個內角等于另一個內角的2倍,那么分四種情況:
①∠EBQ=2∠E=90°,則∠E=45°,∠A=2∠E=90°;
②∠EBQ=2∠Q=90°,則∠Q=45°,∠E=45°,∠A=2∠E=90°;
③∠Q=2∠E,則90°﹣![]() ∠A=∠A,解得∠A=60°;
∠A=∠A,解得∠A=60°;
④∠E=2∠Q,則![]() ∠A=2(90°﹣
∠A=2(90°﹣![]() ∠A),解得∠A=120°.
∠A),解得∠A=120°.
綜上所述,∠A的度數是90°或60°或120°.


科目:初中數學 來源: 題型:
【題目】已知y-2與x+1成正比例函數關系,且x=-2時,y=6.
(1)寫出y與x之間的函數解析式;
(2)求當x=-3時,y的值;
(3)求當y=4時,x的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知BC∥GE,AF∥DE,∠1=50°.
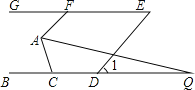
(1)求∠AFG的度數;
(2)若AQ平分∠FAC,交BC于點Q,且∠Q=15°,求∠ACB的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】推理填空:
如圖,已知∠1=∠2,∠B=∠C,可推得AB∥CD.理由如下:
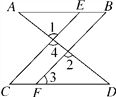
∵∠1=∠2(已知),且∠1=∠4(____________),
∴∠2=∠4(等量代換),
∴CE∥BF(__________________________),
∴∠________=∠3(______________________).
又∵∠B=∠C(已知),
∴∠3=∠B(等量代換).
∴AB∥CD(__________________________).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在Rt△ABC中,∠ACB=90°,E為AC上一點,且AE=BC,過點A作AD⊥CA,垂足為A,且AD=AC,AB、DE交于點F.試判斷線段AB與DE的數量關系和位置關系,并說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知關于x、y的方程組![]() .
.
(1)當a滿足22a+3﹣22a+1=96時,求方程組的解;
(2)當程組的解滿足x+y=16時,求a的值;
(3)試說明:不論a取什么實數,x的值始終為正數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】若如圖,已知AD∥BC,按要求完成下列各小題(保留作圖痕跡,不要求寫作法).
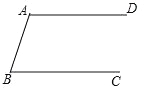
(1)用直尺和圓規作出∠BAD的平分線AP,交BC于點P.
(2)在(1)的基礎上,若∠APB=55°,求∠B的度數.
(3)在(1)的基礎上,E是AP的中點,連接BE并延長,交AD于點F,連接PF.求證:四邊形ABPF是菱形.
查看答案和解析>>
科目:初中數學 來源: 題型:
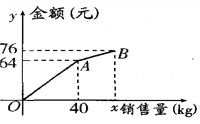
【題目】小李以0.8元/kg的價格從批發市場購進若干千克西瓜到市場去銷售,在銷售了部分西瓜之后,余下的每千克降價0.4元,全部售完,銷售金額與銷售量之間的關系如圖所示,那么小李賺了__________元
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com