
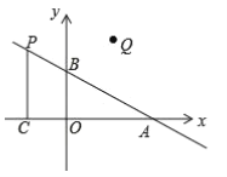
【題目】如圖,在平面直角坐標系中,0是坐標原點,點A坐標為(2, 0),點B坐標為(0, b) (b>0), 點P是直線AB上位于第二象限內的一個動點,過點P作PC垂直于x軸于點C,記點P關于y軸的對稱點為Q.
(1)當b=1時:①求直線AB相應的函數表達式:②若![]() ,求點P的坐標:
,求點P的坐標:
(2)設點P的橫坐標為a,是否同時存在a、b,使得![]() 是等腰直角三角形?若存在,求出所有滿足條件的a、b的值;若不存在,請說明理由.
是等腰直角三角形?若存在,求出所有滿足條件的a、b的值;若不存在,請說明理由.
【答案】(1)①![]() ;②P(
;②P(![]() );(2)存在,a=-2,b=2;或a=
);(2)存在,a=-2,b=2;或a=![]() ,b=1.
,b=1.
【解析】
(1)①由題意確定出B坐標,設直線AB解析式為y=kx+b,把A與B坐標代入求出k與b的值,即可求出AB解析式;②由QO=QA以及OA的長,確定出Q橫坐標,根據P與Q關于y軸對稱,得出P橫坐標,代入直線AB解析式求出縱坐標,即可確定出P坐標;
(2)同時存在a、b,使得△QAC是等腰直角三角形,分兩種情況考慮:①若∠QAC=90°;②若∠AQC=90°,分別求出a與b的值即可.
解:(1)①當b=1時,B(0,1)
由A(2,0),B(0,1),
設直線AB解析式為![]() ,
,
把A與B坐標代入得:
![]() ,
,
解得: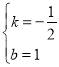
則直線AB解析式為![]()
②∵A(2,0),
∴ OA=2
∵QA=QO,OA=2,
∴Q點橫坐標為xQ=1,
∵點P關于y軸的對稱點為Q,
∴P點的橫坐標為xP=-1,
代入直線AB解析式![]() ,
,
得![]() ,
,
則P坐標得P(![]() )
)
(2)①若∠QAC=90°,如圖1所示,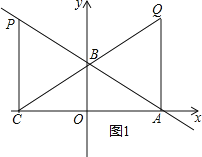
∴Q點的橫坐標為xQ=2,
∴P點的橫坐標為a=xP=-2,
∴AC=AQ=4,
∴Q(2,4)
即P(-2,4),
設直線AP的解析式為![]()
將P(-2,4),A(2,0)代入得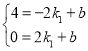
解得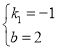
∴直線AP解析式為![]() ,
,
∴a=-2,b=2;
②如圖2,若∠AQC=90°且QA=QC時,過點Q作QH⊥x軸于點H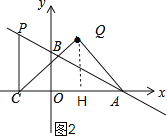
∴QH=CH=AH=![]() AC,
AC,
∴P點的橫坐標為a,
∴Q點的橫坐標為-a,
Q的橫坐標![]() ,解得a=
,解得a=![]() ,-a=
,-a=![]()
Q的縱坐標QH=![]() AC=
AC=![]() =
=![]()
∴Q(![]() ,
,![]() ),P(
),P(![]() ,
,![]() )
)
設直線AP的解析式為![]()
將P(![]() ,
,![]() ),A(2,0)代入得
),A(2,0)代入得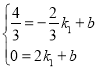
解得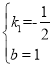
∴直線AP解析式為![]() ,
,
∴b=1,
∴a=![]() ,b=1,
,b=1,
綜上所示,∴a=-2,b=2;或a=![]() ,b=1.
,b=1.


科目:初中數學 來源: 題型:
【題目】(2017浙江省嘉興市,第20題,8分)如圖,一次函數![]() (
(![]() )與反比例函數
)與反比例函數![]() (
(![]() )的圖象交于點A(﹣1,2),B(m,﹣1).
)的圖象交于點A(﹣1,2),B(m,﹣1).
(1)求這兩個函數的表達式;
(2)在x軸上是否存在點P(n,0)(n>0),使△ABP為等腰三角形?若存在,求n的值;若不存在,說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一手機經銷商計劃購進華為品牌![]() 型、
型、![]() 型、
型、![]() 型三款手機共
型三款手機共![]() 部,每款手機至少要購進
部,每款手機至少要購進![]() 部,且恰好用完購機款61000元.設購進
部,且恰好用完購機款61000元.設購進![]() 型手機
型手機![]() 部,
部,![]() 型手機
型手機![]() 部.三款手機的進價和預售價如下表:
部.三款手機的進價和預售價如下表:
手機型號 |
|
|
|
進價(單位:元/部) |
|
|
|
預售價(單位:元/部) |
|
|
|
(1)求出![]() 與
與![]() 之間的函數關系式;
之間的函數關系式;
(2)假設所購進手機全部售出,綜合考慮各種因素,該手機經銷商在購銷這批手機過程中需另外支出各種費用共1500元.
①求出預估利潤W(元)與x(部)之間的關系式;
(注;預估利潤W=預售總額![]() 購機款
購機款![]() 各種費用)
各種費用)
②求出預估利潤的最大值,并寫出此時購進三款手機各多少部.
查看答案和解析>>
科目:初中數學 來源: 題型:
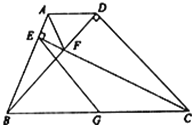
【題目】如圖,四邊形ABCD中,AD∥BC,∠DCB=45°,CD=2,BD⊥CD.過點C作CE⊥AB于E,交對角線BD于F,點G為BC中點,連接EG、AF.
(1)求EG的長;
(2)求證:CF=AB+AF.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】用黑白兩種顏色的正方形紙片,按黑色紙片數逐漸加1的規律拼成一系列圖案,請仔細觀察,并回答下列問題:

(1)第4個圖案中有白色紙片多少張?
(2)第n個圖案中有白色紙片多少張?
(3)第幾個圖案有白色紙片有2011張?(寫出必要的步驟)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某鐵路橋長1000米.現有一列火車從橋上勻速通過.測得火車從開始上橋到完全通過橋共用了1分鐘(即從車頭進入橋頭到車尾離開橋尾),整個火車完全在橋上的時間為40秒.
(1)如果設這列火車的長度為x米,填寫下表(不需要化簡):
火車行駛過程 | 時間(秒) | 路程(米) | 速度(米/秒) |
完全通過橋 | 60 | ||
整列車在橋上 | 40 |
(2)求這列火車的長度.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某地區在一次九年級數學做了檢測中,有一道滿分8分的解答題,按評分標準,所有考生的得分只有四種:0分,3分,5分,8分.老師為了了解學生的得分情況與題目的難易情況,從全區4500名考生的試卷中隨機抽取一部分,通過分析與整理,繪制了如下兩幅圖不完整的統計圖.
請根據以上信息解答下列問題:
(1)填空:a= ,b= ,并把條形統計圖補全;
(2)請估計該地區此題得滿分(即8分)的學生人數;
(3)已知難度系數的計算公式為L=![]() ,其中L為難度系數,X為樣本平均得分,W為試題滿分值.一般來說,根據試題的難度系數可將試題分為以下三類:當0<L≤0.4時,此題為難題;當0.4<L≤0.7時,此題為中等難度試題;當0.7<L<1時,此題為容易題.試問此題對于該地區的九年級學生來說屬于哪一類?
,其中L為難度系數,X為樣本平均得分,W為試題滿分值.一般來說,根據試題的難度系數可將試題分為以下三類:當0<L≤0.4時,此題為難題;當0.4<L≤0.7時,此題為中等難度試題;當0.7<L<1時,此題為容易題.試問此題對于該地區的九年級學生來說屬于哪一類?

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,第一個圖形是一個六邊形,第二個圖形是兩個六邊形組成,依此類推:

(1)寫出第n個圖形的頂點數(n是正整數);
(2)第12個圖有幾個頂點?
(3)若有122個頂點,那么它是第幾個圖形
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com