【題目】如圖，方格紙中的每個小方格都是邊長為1個單位的正方形，在建立平面直角坐標系后，點A、B、C均在格點上．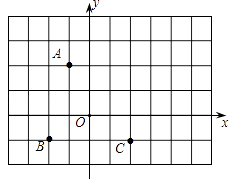
（1）請直接寫出點A、B、C的坐標；
（2）若平移線段AB，使B移動到C的位置，請在圖中畫出A移動后的位置D，依次連接B、C、D、A，并求出四邊形ABCD的面積．
暑假作業海燕出版社系列答案科目：初中數學 來源： 題型：
【題目】已知拋物線y=ax2+bx+3的對稱軸是直線x=1．
（1）求證：2a+b=0；
（2）若關于x的方程ax2+bx﹣8=0的一個根為4，求方程的另一個根．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】拋物線
（
）的對稱軸為直線
，與x軸的一個交點A在點
和
之間，其部分圖象如圖，則下列4個結論：①
；②2a
b=0；③
；④點M（
， 
）、N（
， 
）在拋物線上，若
，
則
，其中正確結論的個數是（ ）.
A. 1個 B. 2個 C. 3個 D. 4個
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某公司員工的月工資如下表：
則這組數據的平均數、眾數、中位數分別為（ ）.
A.2200元、1800元、1600元
B.2000元、1600元、1800元
C.2200元、1600元、1800元
D.1600元、1800元、1900元
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在平面直角坐標系中，A（1，1），B（﹣1，1），C（﹣1，﹣2），D（1，﹣2），把一條長為2016個單位長度且沒有彈性的細線（線的粗細忽略不計）的一端固定在點A處，并按A→B→C→D→A…的規律繞在四邊形ABCD的邊上，則細線另一端所在位置的點的坐標是（ ）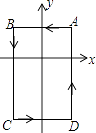
A.（﹣1，0）
B.（1，﹣2）
C.（1，1）
D.（0，﹣2）
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】甲、乙、丙三人之間相互傳球，球從一個人手中隨機傳到另外一個人手中，共傳球三次．
（1）若開始時球在甲手中，求經過三次傳球后，球傳回甲手中的概率是多少？
（2）若丙想使球經過三次傳遞后，球落在自己手中的概率最大，丙會讓球開始時在誰手中？請說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，已知AB∥CD，分別探究下面兩個圖形中∠APC和∠PAB、∠PCD的關系，請從你所得兩個關系中選出任意一個，說明你探究的結論的正確性． 
結論：
（1）
（2） 選擇結論： ， 說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在平面直角坐標系中，△ABC三個頂點的坐標分別為A（﹣4，﹣1）、B（﹣2，3）、C（2，0），將△ABC先向右平移5個單位，再向上平移3個單位，得到△A1B1C1 ．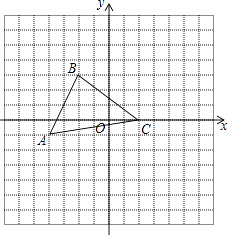 
（1）畫出△A1B1C1；
（2）寫出點A1 ， B1 ， C1的坐標．
（3）求△ABC的面積．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，已知直線AB、CD被直線EF所截，FG平分∠EFD，∠1=∠2=80°，求∠BGF的度數． 解：因為∠1=∠2=80°（已知），
所以AB∥CD（）
所以∠BGF+∠3=180°（）
因為∠2+∠EFD=180°（鄰補角的性質）．
所以∠EFD= ． （等式性質）．
因為FG平分∠EFD（已知）．
所以∠3=∠EFD（角平分線的性質）．
所以∠3= ． （等式性質）．
所以∠BGF= ． （等式性質）．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
