
【題目】如圖(1),將兩塊直角三角尺的直角頂點C疊放在一起,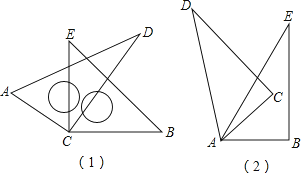
(1)若∠DCE=25°,∠ACB=?;若∠ACB=150°,則∠DCE=?;
(2)猜想∠ACB與∠DCE的大小有何特殊關系,并說明理由;
(3)如圖(2),若是兩個同樣的直角三角尺60°銳角的頂點A重合在一起,則∠DAB與∠CAE的大小又有何關系,請說明理由.
【答案】
(1)
【解答】∵∠ECB=90°,∠DCE=25°
∴∠DCB=90°﹣25°=65°
∵∠ACD=90°
∴∠ACB=∠ACD+∠DCB=155°.
∵∠ACB=150°,∠ACD=90°
∴∠DCB=150°﹣90°=60°
∵∠ECB=90°
∴∠DCE=90°﹣60°=30°.
故答案為:155°,30°
(2)
【解答】猜想得:∠ACB+∠DCE=180°(或∠ACB與∠DCE互補)
理由:∵∠ECB=90°,∠ACD=90°
∴∠ACB=∠ACD+∠DCB=90°+∠DCB
∠DCE=∠ECB﹣∠DCB=90°﹣∠DCB
∴∠ACB+∠DCE=180°
(3)
【解答】∠DAB+∠CAE=120°
理由如下:
∵∠DAB=∠DAE+∠CAE+∠CAB
故∠DAB+∠CAE=∠DAE+∠CAE+∠CAB+∠CAE=∠DAC+∠BAE=120°.
【解析】(1)本題已知兩塊直角三角尺實際就是已知三角板的各個角的度數,根據角的和差就可以求出∠ACB,∠DCE的度數;(2)根據前個小問題的結論猜想∠ACB與∠DCE的大小關系,結合前問的解決思路得出證明.(3)根據(1)(2)解決思路確定∠DAB與∠CAE的大小并證明.


科目:初中數學 來源: 題型:
【題目】如圖,在正方形網格上有一個△DEF .
①作△DEF關于直線HG的軸對稱圖形;
②作△DEF的EF邊上的高;
③若網格上的最小正方形邊長為1,求△DEF的面積.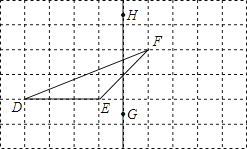
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC和△A′B′C′關于直線m對稱,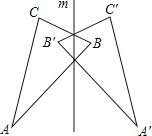
①結合圖形指出對稱點.
②連接A、A′ , 直線m與線段AA′有什么關系?
③延長線段AC與A′C′ , 它們的交點與直線m有怎樣關系?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】我州某養殖場計劃購買甲、乙兩種魚苗600條,甲種魚苗每條16元,乙種魚苗每條20元,相關資料表明:甲、乙兩種魚苗的成活率為80%,90%
(1)若購買這兩種魚苗共用去11000元,則甲、乙兩種魚苗各購買多少條?
(2)若要使這批魚苗的總成活率不低于85%,則乙種魚苗至少購買多少條?
(3)在(2)的條件下,應如何選購魚苗,使購買魚苗的總費用最低?最低費用是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】Pn表示n邊形的對角線的交點個數(指落在其內部的交點),如果這些交點都不重合,那么Pn與n的關系式是:Pn=![]() (其中a,b是常數,n≥4)
(其中a,b是常數,n≥4)
(1)通過畫圖,可得:四邊形時,P4= ;五邊形時,P5= ;
(2)請根據四邊形和五邊形對角線交點的個數,結合關系式,求a,b的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某班要推選學生參加學校的“詩詞達人”比賽,有7名學生報名參加班級選拔賽,他們的選拔賽成績各不相同,現取其中前3名參加學校比賽.小紅要判斷自己能否參加學校比賽,在知道自己成績的情況下,還需要知道這7名學生成績的( )
A.眾數B.中位數C.平均數D.方差
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】計算:
(1)![]() = ,
= , ![]() = ,
= , ![]() = ,
= , ![]() = ,
= , ![]() = ,
= ,
(2)根據計算結果,回答: ![]() 一定等于a嗎?你發現其中的規律了嗎?請你用自己的語言描述出來.
一定等于a嗎?你發現其中的規律了嗎?請你用自己的語言描述出來.
(3)利用你總結的規律,計算: ![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com