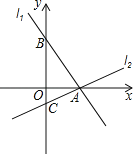
【題目】如圖，過點A（2，0）的兩條直線l1，l2分別交y軸于點B，C，其中點B在原點上方，點C在原點下方，已知AB=
．
（1）求點B的坐標；
（2）若△ABC的面積為4，求直線l2的解析式．
【答案】（1）點B的坐標為（0，3）；（2）l2的解析式為y=
x-1.
【解析】（1）先根據勾股定理求得BO的長，再寫出點B的坐標；（2）先根據△ABC的面積4，求得CO的長，再根據點A、C的坐標運用待定系數法求得直線l2的解析式.
解：（1）∵點A（2，0），AB=
∴BO=
=3
∴點B的坐標為（0，3）；
（2）∵△ABC的面積為4 ∴×BC×AO=4 ∴×BC×2=4，即BC=4
∵BO=3 ∴CO=4﹣3=1 ∴C（0，﹣1）
設l2的解析式為y=kx+b，則
，解得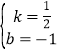
，
∴l2的解析式為y=x﹣1．
“點睛”本題主要考查了兩條直線的交點問題，解題的關鍵是掌握勾股定理以及待定系數法.注意：兩條直線的交點坐標，就是由這兩條直線相對應的一次函數的表達式所組成二元一次過程組的解，反之也成立.
全能測控期末小狀元系列答案科目：初中數學 來源： 題型：
【題目】如圖所示，AB⊥BC，CD⊥BC，垂足分別為B、C，AB=BC，E為BC的中點，且AE⊥BD于F，若CD=4cm，則AB的長度為（ ）
A. 4cm B. 8cm C. 9cm D. 10cm
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知：直線AB∥CD，點M，N分別在直線AB，CD上，點E為平面內一點.
(1)如圖1，∠BME，∠E，∠END的數量關系為 (直接寫出答案)；
(2)如圖2，∠BME＝m°，EF平分∠MEN，NP平分∠END，EQ∥NP，求∠FEQ的度數(用用含m的式子表示)
(3)如圖3，點G為CD上一點，∠BMN＝n·∠EMN，∠GEK＝n·∠GEM，EH∥MN交AB于點H，探究∠GEK，∠BMN，∠GEH之間的數量關系(用含n的式子表示)
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，已知拋物線與x軸交于A（﹣1，0）、B（4，0）兩點，與y軸交于點C（0，3）．
（1）求拋物線的解析式；
（2）在x軸下方的拋物線上是否存在一點P，使△PAB的面積等于△ABC的面積？若存在，求出點P的坐標；若不存在，請說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
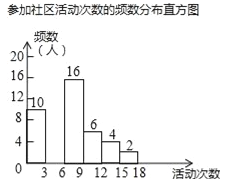
【題目】某校為了解全校學生上學期參加社區活動的情況，學校隨機調查了本校50名學生參加社區活動的次數，并將調查所得的數據整理如下：
參加社區活動次數的頻數、頻率分布表
根據以上圖表信息，解答下列問題：
（1）表中a= ，b= ；
（2）請把頻數分布直方圖補充完整（畫圖后請標注相應的數據）；
（3）若該校共有1200名學生，請估計該校在上學期參加社區活動超過6次的學生有多少人？
查看答案和解析>>
科目：初中數學 來源： 題型：
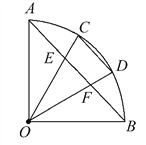
【題目】如圖,∠AOB=90°,C,D是
的三等分點,AB分別交OC,OD于點E,F.試找出圖中相等的線段(半徑除外).
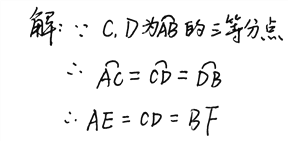
(1)錯因: .
(2)糾錯:____________________________________________________________
.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知二次函數y=a(x2)2+3的圖象經過點(1,0).
(1)求這個二次函數的解析式；
(2)分別指出這個二次函數圖象的開口方向、對稱軸和頂點坐標.
(3) 寫出把此拋物線向右平移1個單位長度，再向上平移2個單位長度后的拋物線解析式。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
