
【題目】如圖,直角坐標(biāo)系中,![]() 的頂點都在網(wǎng)格點上,其中,
的頂點都在網(wǎng)格點上,其中,![]() 點坐標(biāo)為
點坐標(biāo)為![]() ,
,
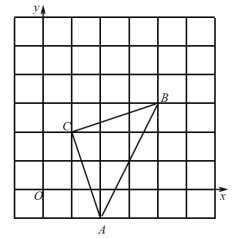
(1)寫出點![]() 、
、![]() 的坐標(biāo):
的坐標(biāo):![]() (____,____)、
(____,____)、![]() (____,____)
(____,____)
(2)將![]() 先向左平移
先向左平移![]() 個單位長度,再向上平移
個單位長度,再向上平移![]() 個單位長度,得到
個單位長度,得到![]() ,畫出
,畫出![]() ;
;
(3)寫出三個頂點坐標(biāo)![]() (___,___)、
(___,___)、![]() (___,___)、
(___,___)、![]() (___,___);
(___,___);
(4)求![]() 的面積.
的面積.

| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在直角坐標(biāo)系中,△ABC滿足∠BCA=90°,AC=BC=![]() ,點A、C分別在x軸和y軸上,當(dāng)點A從原點開始沿x軸的正方向運(yùn)動時,則點C始終在y軸上運(yùn)動,點B始終在第一象限運(yùn)動.
,點A、C分別在x軸和y軸上,當(dāng)點A從原點開始沿x軸的正方向運(yùn)動時,則點C始終在y軸上運(yùn)動,點B始終在第一象限運(yùn)動.
(1)當(dāng)AB∥y軸時,求B點坐標(biāo).
(2)隨著A、C的運(yùn)動,當(dāng)點B落在直線y=3x上時,求此時A點的坐標(biāo).
(3)在(2)的條件下,在y軸上是否存在點D,使以O、A、B、D為頂點的四邊形面積是4?如果存在,請直接寫出點D的坐標(biāo);如果不存在,請說明理由.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
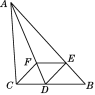
【題目】如圖,在△ABC中,∠BAC的平分線交BC于點D,E是AB上一點,且AE=AC,EF∥BC交AD于點F.
求證:四邊形CDEF是菱形.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】[閱讀]
在平面直角坐標(biāo)系中,以任意兩點P( x1,y1)、Q(x2,y2)為端點的線段中點坐標(biāo)為(![]() ,
,![]() ).
).
[運(yùn)用]
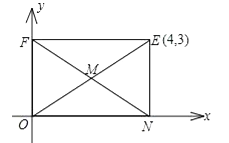
(1)如圖,矩形ONEF的對角線相交于點M,ON、OF分別在x軸和y軸上,O為坐標(biāo)原點,點E的坐標(biāo)為(4,3),則點M的坐標(biāo)為 .
(2)在直角坐標(biāo)系中,有A(﹣1,2),B(3,1),C(1,4)三點,另有一點D與點A、B、C構(gòu)成平行四邊形的頂點,求點D的坐標(biāo).
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
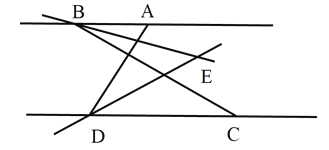
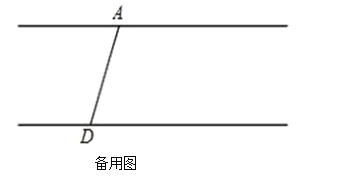
【題目】AB∥CD,C在 D的右側(cè),BE平分∠ABC,DE平分∠ADC,BE、DE所在的直線交于點 E.∠ADC=70°.
(1)求∠EDC 的度數(shù);
(2)若∠ABC=30°,求∠BED 的度數(shù);
(3)將線段 BC沿 DC方向移動,使得點 B在點 A的右側(cè),其他條件不變,若∠ABC=n°,請直接寫出∠BED 的度數(shù)(用含 n的代數(shù)式表示).
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】重慶市居民用水的水價實行階梯收費(fèi),標(biāo)準(zhǔn)如下表:
每戶居民每月用水量 | 水費(fèi)單價(元) |
|
|
|
|
| 4.5 |
(1)已知張三家5月份用水13噸,繳費(fèi)47元,6月份用水15噸,繳費(fèi)55元.請根據(jù)上述信息,求![]() 、
、![]() 的值.
的值.
(2)在(1)的條件下,由于天氣變熱,7月份是用水高峰期,張三家計劃7月份水費(fèi)支出不超過100元,那么張三家7月份最多可用多少噸水?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
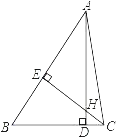
【題目】如圖,△ABC中,AD⊥BC,CE⊥AB,垂足分別為D、E,AD、CE交于點H,請你添加一個適當(dāng)?shù)臈l件:_____,使△AEH≌△CEB.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖①所示是一個長為![]() ,寬為
,寬為![]() 的長方形,沿圖中虛線用剪刀均分成四個小長方形,然后按圖②的方式拼成一個正方形.
的長方形,沿圖中虛線用剪刀均分成四個小長方形,然后按圖②的方式拼成一個正方形.
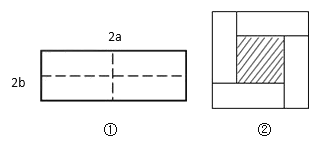
(1)圖②中的陰影部分的正方形的邊長等于 .(用含![]() ,
,![]() 的代數(shù)式表示)
的代數(shù)式表示)
(2)請用兩種不同的方法列代數(shù)式表示圖②中陰影部分的面積:
方法①: .
方法②: .
(3)觀察圖②,直接寫出![]() 、
、![]() 、
、![]() 這三個代數(shù)式之間的等量關(guān)系.
這三個代數(shù)式之間的等量關(guān)系.
(4)根據(jù)(3)題中的等量關(guān)系,若![]() ,
,![]() ,求圖②中陰影部分的面積.
,求圖②中陰影部分的面積.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
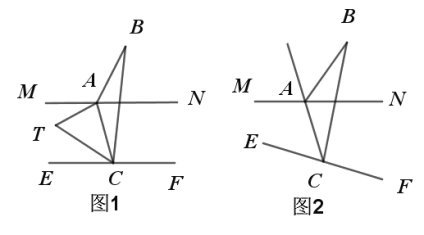
【題目】已知點A和點C分別在直線MN和直線EF上,點B在直線外,∠BAN=α,∠BCF=β.
(1)如圖1,若MN∥EF,則∠B= (用α,β的式子表示,不寫證明過程)
(2)在(1)的條件下,點T在直線MN與直線EF之間,∠MAT=![]() ∠BAN,∠TCB=2∠TCE,求∠B與∠T之間的數(shù)量關(guān)系.
∠BAN,∠TCB=2∠TCE,求∠B與∠T之間的數(shù)量關(guān)系.
(3)如圖2,若MN不平行于EF,直線AC平分∠MAB,且平分∠ECB,則∠B= (用α,β的式子表示,不寫證明過程)
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com