
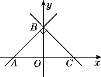
【題目】如圖,直線y=x+2與x軸交于點A,與y軸交于點B,AB⊥BC,且點C在x軸上,若拋物線y=ax2+bx+c以C為頂點,且經過點B,求這條拋物線對應的函數表達式.
 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
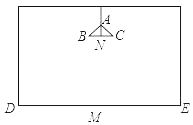
【題目】在長、寬都為4m,高為3m的房間的正中央的天花板上懸掛著一只白熾燈泡,為了集中光線,加上了燈罩(如圖所示).已知燈罩深AN=8cm,燈泡離地面2m,為了使光線恰好照在墻角D、E處,燈罩的直徑BC應為多少?(結果保留兩位小數,![]() ≈1.414)
≈1.414)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】鳳城商場經銷一種高檔水果,售價為每千克50元
(1)連續兩次降價后售價為每千克32元,若每次下降的百分率相同.求平均下降的百分率;
(2)已知這種水果的進價為每千克40元,每天可售出500千克,經市場調查發現,若每千克漲價1元,日銷售量將減少20千克,每千克應漲價多少元才能使每天獲得的利潤最大?
查看答案和解析>>
科目:初中數學 來源: 題型:
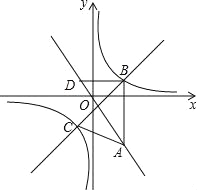
【題目】如圖,在平面直角坐標系xOy中,點A(a,﹣![]() )在直線y=﹣
)在直線y=﹣![]() 上,AB∥y軸,且點B的縱坐標為1,雙曲線y=
上,AB∥y軸,且點B的縱坐標為1,雙曲線y=![]() 經過點B.
經過點B.
(1)求a的值及雙曲線y=![]() 的解析式;
的解析式;
(2)經過點B的直線與雙曲線y=![]() 的另一個交點為點C,且△ABC的面積為
的另一個交點為點C,且△ABC的面積為![]() .
.
①求直線BC的解析式;
②過點B作BD∥x軸交直線y=﹣![]() 于點D,點P是直線BC上的一個動點.若將△BDP以它的一邊為對稱軸進行翻折,翻折前后的兩個三角形所組成的四邊形為正方形,直接寫出所有滿足條件的點P的坐標.
于點D,點P是直線BC上的一個動點.若將△BDP以它的一邊為對稱軸進行翻折,翻折前后的兩個三角形所組成的四邊形為正方形,直接寫出所有滿足條件的點P的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,拋物線y=ax2+bx+c經過A(﹣2,﹣4),O(0,0),B(2,0)三點.
(1)求拋物線y=ax2+bx+c的解析式;
(2)若點M是該拋物線對稱軸上的一點,求AM+OM的最小值.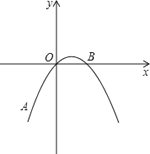
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在Rt△ABC中,∠ABC=90°,以AB為直徑作半圓⊙O交AC于點D,點E為BC的中點,連接DE.

(1)求證:DE是半圓⊙O的切線;
(2)若∠BAC=30°,DE=2,求AD的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,某大學的樓門是一拋物線形水泥建筑物,大門的地面寬度為![]() ,兩側距離地面
,兩側距離地面![]() 高處各有一個掛校名橫匾用的鐵環,兩鐵環的水平距離為
高處各有一個掛校名橫匾用的鐵環,兩鐵環的水平距離為![]() ,則校門的高約為(精確到
,則校門的高約為(精確到![]() ,水泥建筑物的厚度忽略不計)( )
,水泥建筑物的厚度忽略不計)( )
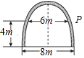
A. 9.2m B. 9.1m C. 9.0m D. 8.9m
查看答案和解析>>
科目:初中數學 來源: 題型:
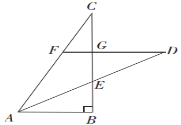
【題目】如圖,在△ABC中,∠ABC=90°,且BC=6,AB=3,AD是∠BAC的平分線,與BC相交于點E,點G是BC上一點,E為線段BG的中點,DG⊥BC于點G,交AC于點F,則FG的長為_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
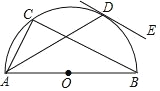
【題目】如圖,△ABC 內接于半⊙O,AB 為直徑,弦 AD 平分∠CAB,DE 切⊙O 于點 D.
(1) 求證:DE∥BC
(2) 若 AD=BC,⊙O 半徑為 2,求∠CAD 與弧CD圍成區域的面積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com