
【題目】如圖,直線y=2x與反比例函數y=![]() (k≠0,x>0)的圖象交于點A(1,a),點B是此反比例函數圖象上任意一點(不與點A重合),BC⊥x軸于點C.
(k≠0,x>0)的圖象交于點A(1,a),點B是此反比例函數圖象上任意一點(不與點A重合),BC⊥x軸于點C.
(1)求k的值;
(2)求△OBC的面積.

【答案】(1)2;(2)1.
【解析】試題分析:(1)由直線y=2x與反比例函數y=![]() (k≠0,x>0)的圖象交于點A(1,a),先將A(1,a)代入直線y=2x求出a的值,從而確定A點的坐標,然后將A點的坐標代入反比例函數y=
(k≠0,x>0)的圖象交于點A(1,a),先將A(1,a)代入直線y=2x求出a的值,從而確定A點的坐標,然后將A點的坐標代入反比例函數y=![]() 中即可求出k的值;(2)由反比例函數y=
中即可求出k的值;(2)由反比例函數y=![]() 的比例系數k的幾何意義,可知△BOC的面積等于
的比例系數k的幾何意義,可知△BOC的面積等于![]() |k|,從而求出△OBC的面積.
|k|,從而求出△OBC的面積.
試題解析:解:(1)∵直線y=2x與反比例函數y=![]() (k≠0,x>0)的圖象交于點A(1,a),先
(k≠0,x>0)的圖象交于點A(1,a),先
∴將A(1,a)代入直線y=2x,得:
a=2
∴A(1,2),
將A(1,2)代入反比例函數y=![]() 中得:k=2,
中得:k=2,
∴y=![]() ;
;
(2)∵B是反比例函數y=![]() 圖象上的點,且BC⊥x軸于點C,
圖象上的點,且BC⊥x軸于點C,
∴△BOC的面積=![]() |k|=
|k|=![]() ×2=1.
×2=1.


科目:初中數學 來源: 題型:
【題目】英國曼徹斯特大學的兩位科學家因為成功地從石墨中分離出石墨烯,榮獲了諾貝爾物理學獎.石墨烯目前是世上最薄卻也是最堅硬的納米材料,同時還是導電性最好的材料,其理論厚度僅0.000 000 000 34米,將這個數用科學記數法表示為
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(8分)如圖,在△ABC中,∠C=60°,∠A=40°.

(1)用尺規作圖作AB的垂直平分線,交AC于點D,交AB于點E(保留作圖痕跡,不要求寫作法和證明);
(2)求證:BD平分∠CBA.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,已知直線PQ∥MN,點A在直線PQ上,點C、D在直線MN上,連接AC、AD,∠PAC=50°,∠ADC=30°,AE平分∠PAD,CE平分∠ACD,AE與CE相交于點E.



(1)若將圖1中的線段AD沿MN向右平移到A1D1如圖2所示位置,此時A1E平分∠AA1D1,CE平分∠ACD1,A1E與CE相交于E,∠PAC=50°,∠A1D1C=30°,求∠A1EC的度數.
(2)若將圖1中的線段AD沿MN向左平移到A1D1如圖3所示位置,其他條件與(1)相同,求此時∠A1EC的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】圖①是一個長為2m,寬為2n的長方形紙片,將長方形紙片沿圖中虛線剪成四個形狀和大小完全相同的小長方形,然后拼成圖②所示的一個大正方形。
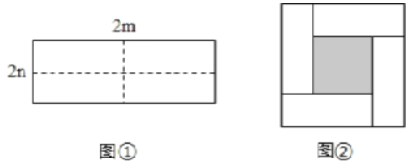
(1)用兩種不同的方法表示圖②中小正方形(陰影部分)的面積:
方法一:![]() ;
;
方法二:![]() .
.
(2)(m+n)![]() ,(mn)
,(mn) ![]() ,mn這三個代數式之間的等量關系為___
,mn這三個代數式之間的等量關系為___
(3)應用(2)中發現的關系式解決問題:若x+y=9,xy=14,求xy的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】4月的某天小欣在“A超市”買了“雀巢巧克力”和“趣多多小餅干”共10包,已知“雀巢巧克力”每包22元,“趣多多小餅干”每包2元,總共花費了80元.
(1)請求出小欣在這次采購中,“雀巢巧克力”和“趣多多小餅干”各買了多少包?
(2)“五一”期間,小欣發現,A、B兩超市以同樣的價格出售同樣的商品,并且又各自推出不同的優惠方案:在A超市累計購物超過50元后,超過50元的部分打九折;在B超市累計購物超過100元后,超過100元的部分打八折.
①請問“五一”期間,若小欣購物金額超過100元,去哪家超市購物更劃算?
②“五一”期間,小欣又到“B超市”購買了一些“雀巢巧克力”,請問她至少購買多少包時,平均每包價格不超過20元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為落實國務院房地產調控政策,使“居者有其屋”,某市加快了廉租房的建設力度.2010年市政府共投資2億元人民幣建設了廉租房8萬平方米,預計到2012年底三年共累計投資9.5億元人民幣建設廉租房,若在這兩年內每年投資的增長率相同.
(1)求每年市政府投資的增長率;
(2)若這兩年內的建設成本不變,求到2012年底共建設了多少萬平方米廉租房.
查看答案和解析>>
科目:初中數學 來源: 題型:
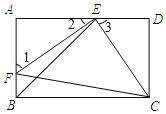
【題目】如圖,E,F分別是矩形ABCD的邊AD,AB上的點,若EF=EC,且EF⊥EC.
(1)求證:△AEF≌△DCE;
(2)若CD=1,求BE的長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com