【題目】如圖，AD是△ABC的中線，E，F分別是AD和AD延長線上的點，且DE＝DF，連接BF，CE，下列說法：①△ABD 和△ACD面積相等；②∠BAD＝∠CAD；③△BDF≌△CDE；④BF∥CE；⑤CE＝AE．其中正確的是（ ）
A. ①② B. ③⑤ C. ①③④ D. ①④⑤
【答案】C
【解析】
根據三角形中線的定義可得BD=CD，根據等底等高的三角形的面積相等判斷出①正確，然后利用“邊角邊”證明△BDF和△CDE全等，根據全等三角形對應邊相等可得CE=BF，全等三角形對應角相等可得∠F=∠CED，再根據內錯角相等，兩直線平行可得BF∥CE．
∵AD是△ABC的中線，
∴BD=CD，
∴△ABD和△ACD面積相等，故①正確；
∵AD為△ABC的中線，
∴BD=CD，∠BAD和∠CAD不一定相等，故②錯誤；
在△BDF和△CDE中，
，
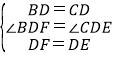∴△BDF≌△CDE（SAS），故③正確；
∴∠F=∠DEC，
∴BF∥CE，故④正確；
∵△BDF≌△CDE，
∴CE=BF，故⑤錯誤，
正確的結論為：①③④，
故選C．
科目：初中數學 來源： 題型：
【題目】定義:若
則稱
與
是關于1的平衡數。
(1)5與______是關于1的平衡數；
(2)
與________是關于1的平衡數(用含
的代數式表示)；
(3)若
判斷與是否是關于1的平衡數,并說明理由。
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖所示，在平面直角坐標系中，A(－1，5)、B(－1，0)、C(－4，3)
(1) 求出△ABC的面積
(2) 在圖形中作出△ABC關于y軸的對稱圖形△A1B1C1，并寫出A1、B1、C1的坐標
(3) 是否存在一點P到AC、AB的距離相等，同時到點A、點B的距離也相等．若存在保留作圖痕跡標出點P的位置，并簡要說明理由；若不存在，請說明理由
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】閱讀下列材料，然后解決問題：和、差、倍、分等問題中有著廣泛的應用，截長法與補短法在證明線段的和、差、倍、分等問題中有著廣泛的應用．具體的做法是在某條線段上截取一條線段等于某特定線段，或將某條線段延長，使之與某特定線段相等，再利用全等三角形的性質等有關知識來解決數學問題．
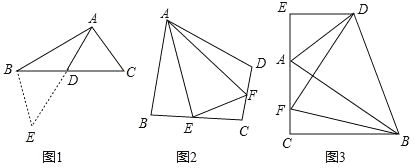
（1）如圖1，在△ABC中，若 AB＝12，AC＝8，求 BC邊上的中線AD的取值范圍．
解決此問題可以用如下方法：延長AD到點E使 DE＝AD，再連接 BE，把AB、AC、2AD集中在△ABE中．利用三角形三邊的關系即可判斷中線 AD的取值范圍是_______.
問題解決：
（2）如圖2，在四邊形ABCD中，AB＝AD，∠ABC+∠ADC＝180°，E、F分別是邊BC，CD上的兩點，且∠EAF＝
∠BAD，求證：BE+DF＝EF．
問題拓展：
（3）如圖3，在△ABC中，∠ACB＝90°，∠CAB＝60°，點D是△ABC 外角平分線上一點，DE⊥AC交 CA延長線于點E，F是 AC上一點，且DF＝DB．
求證：AC﹣AE＝AF．
查看答案和解析>>
科目：初中數學 來源： 題型：
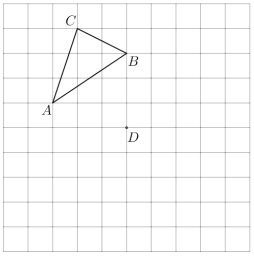
【題目】在圖中網格上按要求畫出圖形，并回答問題：
（1）如果將三角形
平移，使得點
平移到圖中點
位置，點
、點
的對應點分別為點
、點
，請畫出三角形
；
（2）畫出三角形關于點成中心對稱的三角形
．
（3）三角形與三角形是否關于某個點成中心對稱？如果是，請在圖中畫出這個對稱中心，并記作點
．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】計算下列各題
（1）3b﹣2a2﹣（﹣4a+a2+3b）+a2；
（2）﹣13﹣（1﹣
）×
×[2﹣（﹣3）2]；
（3）﹣|﹣23|+15﹣|4.5﹣（﹣2.5）|；
（4）89′25″﹣48′58″；
（5）化簡求值：5（3a2b﹣ab2）﹣（ab2+3a2b），其中a＝，b＝．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】(1)已知多項式
x2ym＋1＋xy2－2x3＋8是六次四項式，單項式－
x3ay5－m的次數與多項式的次數相同，求m，a的值；
(2)已知多項式mx4＋(m－2)x3＋(2n＋1)x2－3x＋n不含x2和x3的項，試寫出這個多項式，再求當x＝－1時多項式的值．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
