
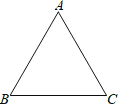
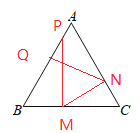
【題目】如圖,在等邊三角形ABC中,AB=5,在AB邊上有一點P,過點P作PM⊥BC,垂足為M,過點M作MN⊥AC,垂足為N,過點N作NQ⊥AB,垂足為Q.當PQ=1時,BP=_____.
【答案】![]() 或
或![]()
【解析】由題意可知P點可能靠近B點,也可能靠近A點,所以需要分為兩種情況:設BM=x,AQ=y,
若P靠近B點,由題意可得∠BPM=30°,根據直角三角形的性質可得BP=2BM=2x,AN=2y,CM=2CN=10-4y,再根據AB=BC=5,PQ=1,列方程組![]() ,解出x、y即可求得BP的長;
,解出x、y即可求得BP的長;
若點P靠近A點,同理可得![]() ,求解即可.
,求解即可.
設BM=x,AQ=y,
若P靠近B點,如圖
∵等邊△ABC,
∴AB=BC=AC=5,∠A=∠B=∠C=60°
∵PM⊥BC
∴∠BMP=90°
則Rt△BMP中,∠BPM=30°,
∴BM=![]() BP
BP
則BP=2x
同理AN=2y,
則CN=5-2y
在Rt△BCM中,CM=2CN=10-4y
∵AB=BC=5,PQ=1
∴![]()
解得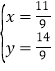
∴BP=2x=![]() ;
;
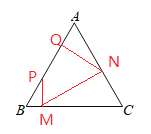
若點P靠近A點,如圖
由上面的解答可得BP=2x,AQ=y,CM=10-4y
∴![]()
解得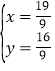
∴BP=2x=![]()
綜上可得BP的長為:![]() 或
或![]() .
.


 小學教材完全解讀系列答案
小學教材完全解讀系列答案科目:初中數學 來源: 題型:
【題目】“五一”期間,申老師一家自駕游去了離家170千米的某地,下面是他們離家的距離y(千米)與汽車行駛時間x(小時)之間的函數關系的圖像.
(1)他們出發半小時后,離家多少千米?
(2)求出AB段的函數表達式.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在四邊形ABCD中,AB=CD,BF=DE,AE⊥BD,CF⊥BD,垂足分別為E,F.

(1)求證:△ABE≌△CDF;
(2)若AC與BD交于點O,求證:AO=CO.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】數學家高斯在上學時曾經研究過這樣一個問題,![]() ?
?
經過研究,這個問題的一般性結論是![]() ,其中
,其中![]() 為正整數,現在我們來研究一個類似的問題:
為正整數,現在我們來研究一個類似的問題:![]() ?
?
觀察下面三個特殊的等式:
![]()
![]()
![]()
將這三個等式的兩邊相加,可以得到![]() .
.
讀完這段材料,請你計算:
(1)![]() ________;(直接寫出結果)
________;(直接寫出結果)
(2)![]() ;(寫出計算過程)
;(寫出計算過程)
(3)![]() ________.
________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,正方形ABCD中,AB=8cm,對角線AC,BD相交于點O,點E,F分別從B,C兩點同時出發,以1cm/s的速度沿BC,CD運動,到點C,D時停止運動,設運動時間為t(s),△OEF的面積為s(cm2),則s(cm2)與t(s)的函數關系可用圖象表示為( )
A.
B.
C.
D.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某公司員工分別住在A、B、C三個住宅區,A區有25人,B區有15人,C區有10人,三個區在一條直線上,位置如圖所示,公司的接送車打算在此間只設一個停靠點,為使所有員工步行到停靠點的路程總和最少,那么停靠點的位置應設在( )

A. A區 B. B區 C. A區或B區 D. C區
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC 中,AB=AC,以AB為直徑作⊙O,與BC交于點D,過D作AC的垂線,垂足為E.證明: 
(1)BD=DC;
(2)DE是⊙O切線.
查看答案和解析>>
科目:初中數學 來源: 題型:
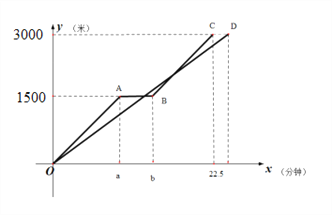
【題目】小軍和爸爸同時從家騎自行車去圖書館,爸爸先以150米/分的速度騎行一段時間,休息了5分鐘,再以m米/分的速度到達圖書館,小軍始終以同一速度騎行,兩人行駛的路程y(米)與時間x(分)的關系如圖所示,請結合圖像,解答下列問題:
(1)a= b= ,m=
(2)若小軍的速度是120米/分,求小軍在途中與爸爸第二次相遇時,距圖書館的距離;
(3)在(2)的條件下,爸爸自第二次出發至到達圖書館前,何時與小軍相距100米?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com