
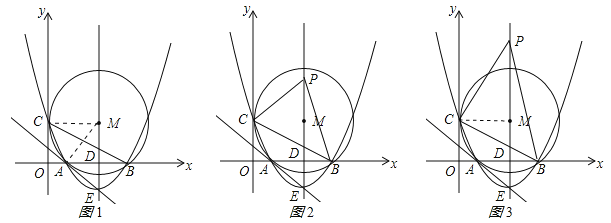
【題目】如圖,在平面直角坐標系中,點M的坐標是(5,4),⊙M與y軸相切于點C,與x軸相交于A、B兩點.
(1)則點A、B、C的坐標分別是A(__,__),B(__,__),C(__,__);
(2)設經過A、B兩點的拋物線解析式為![]() ,它的頂點為F,求證:直線FA與⊙M相切;
,它的頂點為F,求證:直線FA與⊙M相切;
(3)在拋物線的對稱軸上,是否存在點P,且點P在x軸的上方,使△PBC是等腰三角形.如果存在,請求出點P的坐標;如果不存在,請說明理由.

【答案】(1)A(2,0),B(8,0),C(0,4);(2)證明見試題解析;(3)P(5,4),或(5,![]() ),或(5,
),或(5,![]() ).
).
【解析】
試題分析:(1)連接MC、MA,由切線的性質得出MC⊥y軸,MC=MA=5,OC=MD=4,得出點C的坐標;由MD⊥AB,得出DA=DB,∠MDA=90°,由勾股定理求出AD,得出BD、OA、OB,即可得出點A、B的坐標;
(2)把點A(2,0)代入拋物線得出k的值,得出頂點E的坐標,得出DE、ME,由勾股定理得出![]() 的值,證出
的值,證出![]() ,由勾股定理的逆定理證出∠MAE=90°,即可得出EA與⊙M相切;
,由勾股定理的逆定理證出∠MAE=90°,即可得出EA與⊙M相切;
(3)由勾股定理求出BC,分三種情況:
①當PB=PC時,點P在BC的垂直平分線上,點P與M重合,容易得出點P的坐標;
②當BP=BC=![]() 時,由勾股定理求出PD,即可得出點P的坐標;
時,由勾股定理求出PD,即可得出點P的坐標;
③當PC=BC=![]() 時,由勾股定理求出PM,得出PD,即可得出點P的坐標.
時,由勾股定理求出PM,得出PD,即可得出點P的坐標.
試題解析:(1)連接MC、MA,如圖1所示:
∵⊙M與y軸相切于點C,∴MC⊥y軸,∵M(5,4),∴MC=MA=5,OC=MD=4,∴C(0,4),∵MD⊥AB,∴DA=DB,∠MDA=90°,∴AD=![]() =3,∴BD=3,∴OA=5﹣3=2,OB=5+3=8,∴A(2,0),B(8,0),故答案為:2,0;8,0;0,4;
=3,∴BD=3,∴OA=5﹣3=2,OB=5+3=8,∴A(2,0),B(8,0),故答案為:2,0;8,0;0,4;
(2)把點A(2,0)代入拋物線y=![]() ,得:k=
,得:k=![]() ,∴E(5,
,∴E(5,![]() ),∴DE=
),∴DE=![]() ,∴ME=MD+DE=
,∴ME=MD+DE=![]() =
=![]() ,
,![]() =
=![]() =
=![]() ,∵
,∵![]() =
=![]() =
=![]() ,
,![]() =
=![]() ,∴
,∴![]() ,∴∠MAE=90°,即EA⊥MA,∴EA與⊙M相切;
,∴∠MAE=90°,即EA⊥MA,∴EA與⊙M相切;
(3)存在;點P坐標為(5,4),或(5,![]() ),或(5,
),或(5,![]() );理由如下:
);理由如下:
由勾股定理得:BC=![]() =
=![]() =
=![]() ,分三種情況:
,分三種情況:
①當PB=PC時,點P在BC的垂直平分線上,點P與M重合,∴P(5,4);
②當BP=BC=![]() 時,如圖2所示:
時,如圖2所示:
∵PD=![]() =
=![]() =
=![]() ,∴P(5,
,∴P(5,![]() );
);
③當PC=BC=![]() 時,連接MC,如圖3所示:
時,連接MC,如圖3所示:
則∠PMC=90°,根據勾股定理得:PM=![]() =
=![]() =
=![]() ,∴PD=
,∴PD=![]() ,∴P(5,
,∴P(5,![]() );
);
綜上所述:存在點P,且點P在x軸的上方,使△PBC是等腰三角形,點P的坐標為(5,4),或(5,![]() ),或(5,
),或(5,![]() ).
).


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:
【題目】如圖,線段AD、FC、EB兩兩相交,連接AB、CD、EF,則∠A+∠B+∠C+∠D+∠E+∠F=( ) 
A.360°
B.240°
C.200°
D.180°
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AB=AC,點D是BC的中點,點E在AD上. 
(1)圖中的全等三角形有;
(2)從你找到的全等三角形中選出其中一對加以證明.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】“六一”兒童節,某玩具超市設立了一個如圖所示的可以自由轉動的轉盤,開展有獎購買活動.顧客購買玩具就能獲得一次轉動轉盤的機會,當轉盤停止時,指針落在哪一區域就可以獲得相應獎品.下表是該活動的一組統計數據.下列說法不正確的是( )
轉動轉盤的次數n | 100 | 150 | 200 | 500 | 800 | 1000 |
落在“鉛筆”區域的次數m | 68 | 108 | 140 | 355 | 560 | 690 |
落在“鉛筆”區域的頻率 | 0.68 | 0.72 | 0.70 | 0.71 | 0.70 | 0.69 |

A.當n很大時,估計指針落在“鉛筆”區域的頻率大約是0.70
B.假如你去轉動轉盤一次,獲得鉛筆的概率大約是0.70
C.如果轉動轉盤2000次,指針落在“文具盒”區域的次數大約有600次
D.轉動轉盤10次,一定有3次獲得文具盒
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】甲、乙、丙三個登山愛好者經常相約去登山,今年1月甲參加了兩次登山活動.
(1)1月1日甲與乙同時開始攀登一座900米高的山,甲的平均攀登速度是乙的1.2倍,結果甲比乙早15分鐘到達頂峰.求甲的平均攀登速度是每分鐘多少米?
(2)1月6日甲與丙去攀登另一座h米高的山,甲保持第(1)問中的速度不變,比丙晚出發0.5小時,結果兩人同時到達頂峰,問甲的平均攀登速度是丙的多少倍?(用含h的代數式表示)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】△ABC中,∠A、∠B、∠C的對邊分別是a、b、c,AB=8,BC=15,CA=17,則下列結論不正確的是( )
A.△ABC是直角三角形,且AC為斜邊
B.△ABC是直角三角形,且∠ABC=90°
C.△ABC的面積是60
D.△ABC是直角三角形,且∠A=60°
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】情景:試根據圖中信息,解答下列問題: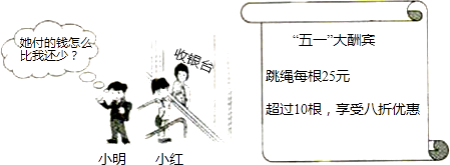
(1)購買6根跳繩需多少元,購買12根跳繩需多少元.
(2)小紅比小明多買2根,付款時小紅反而比小明少5元,你認為有這種可能嗎?若有,請求出小紅購買跳繩的根數;若沒有請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com