Question

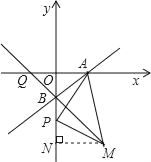
【題目】已知：如圖，平面直角坐標系xOy中，點A、B的坐標分別為A（2，0），B（0，﹣2），P為y軸上B點下方一點，以AP為邊作等腰直角三角形APM，其中PM＝PA，點M落在第四象限，過M作MN⊥y軸于N．

（1）求直線AB的解析式；

（2）求證：△PAO≌△MPN；

（3）若PB＝m（m＞0），用含m的代數式表示點M的坐標；

（4）求直線MB的解析式．

Answer 1

【答案】（1）y＝x﹣2．（2）詳見解析；（3）（2+m，﹣4﹣m）；（4）y＝﹣x﹣2．

【解析】

（1）直線AB的解析式為y＝kx+b（k≠0），利用待定系數法求函數的解析式即可；

（2）先證∠APO＝∠PMN，用AAS證△PAO≌△MPN；

（3）由（2）中全等三角形的性質得到OP＝NM，OA＝NP．根據PB＝m，用m表示出NM和ON＝OP+NP，根據點M在第四象限，表示出點M的坐標即可．

（4）設直線MB的解析式為y＝nx﹣2，根據點M（m+2，﹣m﹣4）．然后求得直線MB的解析式．

（1）解：設直線AB：y＝kx+b（k≠0）

代入A（2，0 ），B （0，﹣2 ），得

，

解得，

∴直線AB的解析式為：y＝x﹣2．

（2）證明：作MN⊥y軸于點N．

∵△APM為等腰直角三角形，PM＝PA，

∴∠APM＝90°．

∴∠OPA+∠NPM＝90°．

∵∠NMP+∠NPM＝90°，

∴∠OPA＝∠NMP．

在△PAO與△MPN中

，

∴△PAO≌△MPN（AAS）．

（3）由（2）知，△PAO≌△MPN，則OP＝NM，OA＝NP．

∵PB＝m（m＞0），

∴ON＝2+m+2＝4+m MN＝OP＝2+m．

∵點M在第四象限，

∴點M的坐標為（2+m，﹣4﹣m）．

（4）設直線MB的解析式為y＝nx﹣2（n≠0）．

∵點M（2+m，﹣4﹣m）．

在直線MB上，

∴﹣4﹣m＝n（2+m）﹣2．

整理，得（m+2）n＝﹣m﹣2．

∵m＞0，

∴m+2≠0．

解得 n＝﹣1．

∴直線MB的解析式為y＝﹣x﹣2．