
【題目】已知:如圖,在Rt△ABC中,∠ACB=90°,AB=5cm,AC=3cm,動點P從點B出發沿射線BC以2cm/s的速度運動,設運動的時間為t秒,
(1)當△ABP為直角三角形時,求t的值:
(2)當△ABP為等腰三角形時,求t的值.
(本題可根據需要,自己畫圖并解答)

【答案】(1)當t=2s或![]() s時,△ABP為直角三角形.(2)當△ABP為等腰三角形時,t=2.5s或4s或
s時,△ABP為直角三角形.(2)當△ABP為等腰三角形時,t=2.5s或4s或![]() s.
s.
【解析】
(1)首先根據勾股定理求出BC的長度,再分兩種情況:①當∠APB為直角時,②當∠BAP為直角時,分別求出此時的t值即可.
(2)當△ABP為等腰三角形時,分三種情況:①當AB=BP時;②當AB=AP時;③當BP=AP時,分別求出BP的長度,繼而可求得t值.
(1)∵∠C=90°,AB=5cm,AC=3cm,
∴BC=4 cm.
①當∠APB為直角時,點P與點C重合,BP=BC=4 cm,
∴t=4÷2=2s.
②當∠BAP為直角時,BP=2tcm,CP=(2t﹣4)cm,AC=3 cm,
在Rt△ACP中,AP2=32+(2t﹣4)2,
在Rt△BAP中,AB2+AP2=BP2,
∴52+[32+(2t﹣4)2]=(2t)2,
解得t=![]() s.
s.
綜上,當t=2s或![]() s時,△ABP為直角三角形.
s時,△ABP為直角三角形.
(2)①當BP=BA=5時,∴t=2.5s.
②當AB=AP時,BP=2BC=8cm,∴t=4s.
③當PB=PA時,PB=PA=2t cm,CP=(4﹣2t)cm,AC=3 cm,
在Rt△ACP中,AP2=AC2+CP2,
∴(2t)2=32+(4﹣2t)2,解得t=![]() s.
s.
綜上,當△ABP為等腰三角形時,t=2.5s或4s或![]() s
s


科目:初中數學 來源: 題型:
【題目】在△ABC中,AB=BC=2,∠ABC=120°,將△ABC繞著點B順時針旋轉角a(0°<a<90°)得到△A1BC;A1B交AC于點E,A1C1分別交AC、BC于D、F兩點.
(1)如圖1,觀察并猜想,在旋轉過程中,線段BE與BF有怎樣的數量關系?并證明你的結論.
(2)如圖2,當a=30°時,試判斷四邊形BC1DA的形狀,并證明.
(3)在(2)的條件下,求線段DE的長度.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,![]() ABC是等邊三角形,點D是線段AC上的一動點,E在BC的延長線上,且BD=DE.
ABC是等邊三角形,點D是線段AC上的一動點,E在BC的延長線上,且BD=DE.
(1)如圖,若點D為線段AC的中點,求證:AD=CE;

(2)如圖,若點D為線段AC上任意一點,求證:AD=CE.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,函數y=![]() (k>0)的圖象經過點A(1,2)、B兩點,過點A作x軸的垂線,垂足為C,連接AB、BC.若三角形ABC的面積為3,則點B的坐標為___________.
(k>0)的圖象經過點A(1,2)、B兩點,過點A作x軸的垂線,垂足為C,連接AB、BC.若三角形ABC的面積為3,則點B的坐標為___________.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,已知 AD 是△ABC 的邊 BC 上的中線.
(1)作出△ABD 的邊 BD 上的高.
(2)若△ABC 的面積為 10,求△ADC 的面積.
(3)若△ABD 的面積為 6,且 BD 邊上的高為 3,求 BC 的長.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,一架梯子AB斜靠在墻面上,且AB的長為2.5米.

(1)若梯子底端離墻角的距離OB為0.7米,求這個梯子的頂端A距地面有多高?
(2)在(1)的條件下,如果梯子的頂端A下滑0.4米到點A′,那么梯子的底端B在水平方向滑動的距離BB′為多少米?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】4張相同的卡片上分別寫有數字2,3,4,5將卡片的背面向上,洗勻后從中任意抽取1 張,將卡片上的數字作為被減數;一只不透明的袋子中裝有標號2,3,4的3個小球,這些球除標號外都相同,攪勻后從中任意摸出一個球,將摸到的球的標號作為減數.
(1)用樹狀圖或列表的方法求這兩個數的差為0的概率;
(2)如果游戲規則規定:當抽到的這兩個數的差為非負數時,則甲獲勝;否則,乙獲勝,你認為這樣的規則公平嗎?如果不公平,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】給出定義,若一個四邊形中存在相鄰兩邊的平方和等于一條對角線的平方,則稱該四邊形為勾股四邊形.
(1)在你學過的特殊四邊形中,寫出兩種勾股四邊形的名稱;
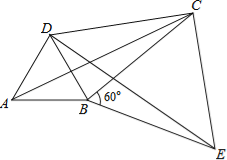
(2)如圖,將△ABC繞頂點B按順時針方向旋轉60°得到△DBE,連接AD,DC,CE,已知∠DCB=30°.
①求證:△BCE是等邊三角形;
②求證:DC2+BC2=AC2,即四邊形ABCD是勾股四邊形.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com