
【題目】如圖,在平面直角坐標系中,已知A(0,5), B(a,b),且a,b滿足b=![]() +
+![]() -1.
-1.
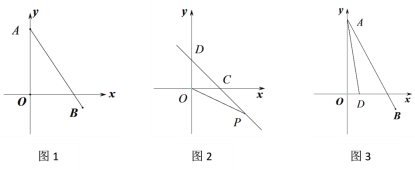
(1)如圖,求線段AB的長;
(2)如圖,直線CD與x軸、y軸正半軸分別交于點C,D,∠OCD=45°,第四象限的點P(m,n)在直線CD上,且mn=-6,求OP2-OC2的值;
(3)如圖,若點D(1,0),求∠DAO +∠BAO的度數.
【答案】(1)![]() ;(2)12 ;(3)45°
;(2)12 ;(3)45°
【解析】
(1)根據b=![]() +
+![]() -1可求得a、b的值,得到B點的坐標,根據兩點間坐標公式即可求解.
-1可求得a、b的值,得到B點的坐標,根據兩點間坐標公式即可求解.
(2)根據直線CD與x軸、y軸正半軸分別交于點C,D,∠OCD=45°,可知直線CD平行于y= -x,可設直線CD解析式為y= -x +b,代入P點坐標,得到m、n、b的關系,代入計算即可.
(3)取點D關于y軸的對稱點![]() ,運用兩點間坐標公式及勾股定理逆定理可判斷△AB
,運用兩點間坐標公式及勾股定理逆定理可判斷△AB![]() 是等腰直角三角形,即可求得∠BA
是等腰直角三角形,即可求得∠BA![]() 的值,等量代換即可.
的值,等量代換即可.
(1)∵b=![]() +
+![]() -1
-1
∴a=4 ,b= -1
∴B點坐標為:(4,-1)
∵A(0,5)
∴AB=![]() )
)![]()
(2)∵直線CD與x軸、y軸正半軸分別交于點C,D,∠OCD=45°
∴直線CD平行于y= -x
設直線CD解析式為y= -x +b
則B點坐標為(b,0)
把點P(m,n)代入得:n= -m +b
∴b= m+n
∴OP2-OC2=![]()
∵mn=-6
∴OP2-OC2![]()
(3)取點D關于y軸的對稱點![]() ,則∠DAO=∠
,則∠DAO=∠![]() ,
,
∴∠DAO +∠BAO=∠![]() +∠BAO=∠BA
+∠BAO=∠BA![]()
∵點D(1,0)
∴![]() (-1,0)
(-1,0)
由(1)得:A(0,5),B(4,-1)
∴A![]() =
=![]() ,
,![]() ,
,![]()
∴A![]() ,
,![]()
∴△A![]() 是等腰直角三角形
是等腰直角三角形
∴∠DAO +∠BAO=∠BA![]() =45°
=45°


 優質課堂快樂成長系列答案
優質課堂快樂成長系列答案科目:初中數學 來源: 題型:
【題目】探究逼近![]() 的有理近似值.
的有理近似值.
方法介紹:
經過![]() 步操作(
步操作(![]() 為正整數)不斷尋找有理數
為正整數)不斷尋找有理數![]() ,
,![]() ,使得
,使得![]() ,并且讓
,并且讓![]() 的值越來越小,同時利用數軸工具將任務幾何化,直觀理解通過等分線段的方法不斷縮小
的值越來越小,同時利用數軸工具將任務幾何化,直觀理解通過等分線段的方法不斷縮小![]() 對應的點
對應的點![]() 所在線段的長度(二分法)
所在線段的長度(二分法)
思路
在數軸上記![]() ,
,![]() 對應的點分別為
對應的點分別為![]() ,
,![]() 和
和![]() 的平均數
的平均數![]() 對應線段
對應線段![]() 的中點(記為
的中點(記為![]() ).通過判斷
).通過判斷![]() 還是
還是![]() ,得到點
,得到點![]() 是在二等分后的“左線段
是在二等分后的“左線段![]() ”上還是“右線段
”上還是“右線段![]() ”上,重復上述步驟,不斷得到
”上,重復上述步驟,不斷得到![]() ,從而得到
,從而得到![]() 更精確的近似值.
更精確的近似值.
具體操作步驟及填寫“閱讀活動任務單”:
(1)當![]() 時,
時,
①尋找左右界值:先尋找兩個連續正整數![]() ,使得
,使得![]() .
.
因為![]() ,所以
,所以![]() ,那么
,那么![]() ,
,![]() ,線段
,線段![]() 的中點
的中點![]() 對應的數
對應的數![]() .
.
②二分定位:判斷點![]() 在“左線段
在“左線段![]() ”上還是在“右線段
”上還是在“右線段![]() ”上.
”上.
比較7與![]() 的大小,從而確定
的大小,從而確定![]() 與
與![]() 的大小;
的大小;
因為![]() >
> ![]() (填 “>”或“<”),得到點
(填 “>”或“<”),得到點![]() 在線段
在線段 ![]() 上(填“
上(填“![]() ”或“
”或“![]() ”).
”).
(2)當![]() 時,在(1)中所得
時,在(1)中所得![]() 的基礎上,仿照以上步驟,繼續進行下去,得到表中
的基礎上,仿照以上步驟,繼續進行下去,得到表中![]() 時的相應內容.
時的相應內容.
請繼續仿照以上步驟操作下去,補全“閱讀活動任務單”:
|
|
|
|
| 點 | 得出更精確的 |
1 | 2 | 3 | 2.5 |
| 點 |
|
2 | 2.5 | 3 | 2.75 |
| 點 |
|
3 | 2.5 | 2.75 | 2.625 |
| ||
4 |
查看答案和解析>>
科目:初中數學 來源: 題型:
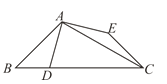
【題目】如圖,△ABC中,∠ABC=45°,∠BCA=30°,點D在BC上,點E在△ABC外,且AD=AE=CE,AD⊥AE,則![]() 的值為____________.
的值為____________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,點E是邊AC上一點,線段BE垂直于∠BAC的平分線于點D,點M為邊BC的中點,連接DM.
(1)求證: DM=![]() CE;
CE;
(2)若AD=6,BD=8,DM=2,求AC的長.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校為美化校園,計劃對面積為1800m2的區域進行綠化,安排甲、乙兩個工程隊完成.已知甲隊每天能完成綠化的面積是乙隊每天能完成綠化的面積的2倍,并且在獨立完成面積為400 m2區域的綠化時,甲隊比乙隊少用4天.
(1)求甲、乙兩工程隊每天能完成綠化的面積分別是多少m2?
(2)若學校每天需付給甲隊的綠化費用是0.4萬元,乙隊為0.25萬元,要使這次的綠化總費用不超過8萬元,至少應安排甲隊工作多少天?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】“五一”期間,小明一家乘坐高鐵前往某市旅游,計劃第二天租用新能源汽車自駕出游,不同租賃公司的租車費用(單位:元)與時間(單位:![]() )之間的關系如圖所示.
)之間的關系如圖所示.

根據以上信息,解答下列問題:
(1)設租車時間為![]() 時,租用甲公司的車所需費用為
時,租用甲公司的車所需費用為![]() 元,租用乙公司的車所需費用為
元,租用乙公司的車所需費用為![]() 元,分別求出
元,分別求出![]() ,
,![]() 關于
關于![]() 的函數解析式;
的函數解析式;
(2)請你幫助小明計算并選擇哪個出游方案合算.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(2016四川省攀枝花市)某市為了鼓勵居民節約用水,決定實行兩級收費制度.若每月用水量不超過14噸(含14噸),則每噸按政府補貼優惠價m元收費;若每月用水量超過14噸,則超過部分每噸按市場價n元收費.小明家3月份用水20噸,交水費49元;4月份用水18噸,交水費42元.
(1)求每噸水的政府補貼優惠價和市場價分別是多少?
(2)設每月用水量為x噸,應交水費為y元,請寫出y與x之間的函數關系式;
(3)小明家5月份用水26噸,則他家應交水費多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】填寫推理理由:
已知:如圖,D,F,E分別是BC,AC,AB上的點,DF∥AB,DE∥AC,試說明∠EDF=∠A.

解:∵DF∥AB ( ),
∴∠A+∠AFD=180° ( ).
∵DE∥AC ( ),
∴∠AFD+∠EDF=180° ( ).
∴∠A=∠EDF ( ).
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com