
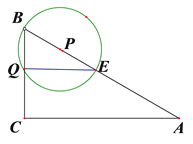
【題目】如圖,在△ABC中,∠ACB為直角,AB=10,![]() °,半徑為1的動圓Q的圓心從點C出發,沿著CB方向以1個單位長度/秒的速度勻速運動,同時動點P從點B出發,沿著BA方向也以1個單位長度/秒的速度勻速運動,設運動時間為t秒(0<t≤5)以P為圓心,PB長為半徑的⊙P與AB、BC的另一個交點分別為E、D,連結ED、EQ.
°,半徑為1的動圓Q的圓心從點C出發,沿著CB方向以1個單位長度/秒的速度勻速運動,同時動點P從點B出發,沿著BA方向也以1個單位長度/秒的速度勻速運動,設運動時間為t秒(0<t≤5)以P為圓心,PB長為半徑的⊙P與AB、BC的另一個交點分別為E、D,連結ED、EQ.
(1)判斷并證明ED與BC的位置關系,并求當點Q與點D重合時t的值;
(2)當⊙P和AC相交時,設CQ為![]() ,⊙P被AC 截得的弦長為
,⊙P被AC 截得的弦長為![]() ,求
,求![]() 關于
關于![]() 的函數; 并求當⊙Q過點B時⊙P被AC截得的弦長;
的函數; 并求當⊙Q過點B時⊙P被AC截得的弦長;
(3)若⊙P與⊙Q相交,寫出t的取值范圍.

【答案】(1)ED⊥BC,![]() ;(2)
;(2)![]() ,
,![]() ;(3)
;(3)![]()
【解析】試題分析:(1)連接PD,由PB=PD,PD=PE,可得∠PBD=∠PDB,∠PDE=∠PED,再由三角形的內角和定理可得∠BDE=∠BDP+∠PDE=90°,即可得DE⊥BC;因DE∥CA,可得△BDE∽△BCA,根據相似三角形的性質可得![]() ,設CQ=CD=t,BD=5-t,BE=2t,代入求得t值即可;設⊙P和AC相交于 M、N,BP=CQ=x,AP=AB-BP=10-x,過點P作PH⊥AC于點 H,在Rt△APH中,可得PH=
,設CQ=CD=t,BD=5-t,BE=2t,代入求得t值即可;設⊙P和AC相交于 M、N,BP=CQ=x,AP=AB-BP=10-x,過點P作PH⊥AC于點 H,在Rt△APH中,可得PH=![]() AP,PH=
AP,PH=![]() (10-x),在Rt△PHN中,即可求得y關于x的函數;如圖,當⊙Q經過B點時, CQ=CB﹣QB=4,將t的值代入即可求得MN的長;(3)當Q⊙P與⊙Q外切時,如圖,此時易知∠QBP=60°,BQ=5-t,PQ=t+1,BP=t,
(10-x),在Rt△PHN中,即可求得y關于x的函數;如圖,當⊙Q經過B點時, CQ=CB﹣QB=4,將t的值代入即可求得MN的長;(3)當Q⊙P與⊙Q外切時,如圖,此時易知∠QBP=60°,BQ=5-t,PQ=t+1,BP=t,![]() ,因從此時起直至停止運動,⊙P與⊙Q都處于相交位置,即可得⊙P與⊙Q相交時t的取值范圍.
,因從此時起直至停止運動,⊙P與⊙Q都處于相交位置,即可得⊙P與⊙Q相交時t的取值范圍.
試題解析:
(1)連接PD,∵B、E、D都在⊙P上
∴PB=PD,∠PBD=∠PDB, PD=PE,∠PDE=∠PED
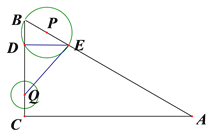
∵△BDE的內角和為180° ∴∠BDE=∠BDP+∠PDE=90°,
∴即:DE⊥BC
∵∠BCA=90°,![]() °
°
∴DE∥CA,∴△BDE∽△BCA,
∴![]()
設CQ=CD=t,BD=5-t,BE=2t
代入有![]() 解得:
解得:![]()
∴當![]() 時Q與D重合.
時Q與D重合.
(2)設⊙P和AC相交于 M、N,

BP=CQ=x,AP=AB-BP=10-x過點P作PH⊥
在Rt△APH中,易知:![]()
PH=![]()
在Rt△PHN中,易知:HN=![]() =
=![]()
![]()
當⊙Q經過B點時,(如圖) CQ=CB﹣QB=4,

將![]() 代入得:
代入得:![]()
(3)當Q⊙P與⊙Q外切時,如圖,
易知此時∠QBP=60°,BQ=5-t,PQ=t+1,BP=t
![]() ,
,
∵從此時起直至停止運動,⊙P與⊙Q都處于相交位置
∴⊙P與⊙Q相交時t的取值范圍為: ![]()


 新課標階梯閱讀訓練系列答案
新課標階梯閱讀訓練系列答案科目:初中數學 來源: 題型:
【題目】某養殖戶的養殖成本逐年增長,已知第一年的養殖成本為12萬元,第3年的養殖成本為17萬元.設每年平均增長的百分率為x,則下面所列方程中正確的是( )
A.12(1﹣x)2=17
B.17(1﹣x)2=12
C.17(1+x)2=12
D.12(1+x)2=17
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(1)如圖,將A、B、C三個字母隨機填寫在三個空格中(每空填一個字母,每空中的字母不重復),請你用畫樹狀圖或列表的方法求從左往右字母順序恰好是A、B、C的概率;
(2)若在如圖三個空格的右側增加一個空格,將A、B、C、D四個字母任意填寫其中(每空填一個字母,每空中的字母不重復),從左往右字母順序恰好是A、B、C、D的概率為 .

查看答案和解析>>
科目:初中數學 來源: 題型:
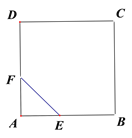
【題目】如圖,E、F分別為正方形ABCD的邊AB、AD上的點,且AE=AF,聯接EF,將△AEF繞點A逆時針旋轉45°,使E落在E![]() ,F落在F
,F落在F![]() ,聯接BE
,聯接BE![]() 并延長交DF
并延長交DF![]() 于點G,如果AB=
于點G,如果AB=![]() ,AE=1,則DG=______.
,AE=1,則DG=______.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,點D是弦AB的中點,點C在⊙O上,CD經過圓心O,則下列結論中不一定正確的是( )
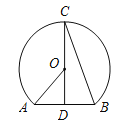
A. CD⊥AB B. ∠OAD =2∠CBD C. ∠AOD =2∠BCD D. 弧AC = 弧BC
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下面的圖象反映的過程是:小明從家去超市買文具,又去書店購書,然后回家.其中x表示時間,y表示小明離他家的距離,若小明家、超市、書店在同一條直線上.
根據圖象回答下列問題: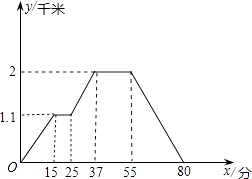
(1)超市離小明家多遠,小明走到超市用了多少時間?
(2)超市離書店多遠,小明在書店購書用了多少時間?
(3)書店離小明家多遠,小明從書店走回家的平均速度是每分鐘多少米?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com