
【題目】如圖,平面直角坐標系中,四邊形![]() 為長方形,其中點
為長方形,其中點![]() 的坐標分別為
的坐標分別為![]() 、
、![]() ,且
,且![]() 軸,交
軸,交![]() 軸于點
軸于點![]() ,
,![]() 交
交![]() 軸于點
軸于點![]() .
.
(1)求![]() 兩點坐標;
兩點坐標;
(2)一動點![]() 從
從![]() 出發,以2個單位/秒的速度沿
出發,以2個單位/秒的速度沿![]() 向
向![]() 點運動(不與
點運動(不與![]() 點重合),在
點重合),在![]() 點運動過程中,連接
點運動過程中,連接![]() ,
,
①試探究![]() 之間的數量關系;并說明理由;
之間的數量關系;并說明理由;
②是否存在某一時刻![]() ,使三角形
,使三角形![]() 的面積等于長方形
的面積等于長方形![]() 面積的
面積的![]() ?若存在,求
?若存在,求![]() 的值并求此時點
的值并求此時點![]() 的坐標;若不存在,請說明理由;
的坐標;若不存在,請說明理由;
③三角形![]() 的面積記作
的面積記作![]() ;三角形
;三角形![]() 的面積記作
的面積記作![]() ;三角形
;三角形![]() 的面積記作
的面積記作![]() ;直接寫出
;直接寫出![]() 、
、![]() 、
、![]() 的關系.
的關系.

科目:初中數學 來源: 題型:
【題目】已知:如圖直線y=![]() x+2與拋物線y=ax2交于A.B兩點,點B的坐標(3,m),直線AB交y軸于點C.
x+2與拋物線y=ax2交于A.B兩點,點B的坐標(3,m),直線AB交y軸于點C.
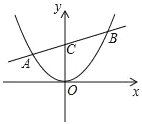

(1)求a,m的值;
(2)點P在對稱軸右側的拋物線上,設P點橫坐標為t,△PAB的面積為s,求s與t的函數關系式;
(3)在(2)的條件下,在x軸上有一點Q,當以B.C.P.Q為頂點的四邊形是平行四邊形時,求點Q的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】有一數值轉換器,原理如圖所示,若開始輸入x的值是7,可發現第1次輸出的結果是12,第2次輸出的結果是6,第3次輸出的結果是 ,依次繼續下去…,第2013次輸出的結果是 .

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,Rt△AOB繞著一點旋轉到△A′OB′的位置,可以看到點A旋轉到點A′,OA旋轉到OA′,∠AOB旋轉到∠A′OB′,這些都是互相對應的點、線段和角.已知∠AOB=30°,∠AOB′=10°,那么點B的對應點是點______;線段OB的對應線段是線段_____;∠A的對應角是______;旋轉中心是點_______;旋轉的角度是______度.
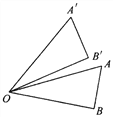
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知關于x的二次函數y=x2-(2m-1)x+m2+3m+4.
(1)探究m取不同值時,二次函數y的圖象與x軸的交點的個數情況;
(2)設二次函數的圖象與x軸的交點為A(x1,0),B(x2,0),且x12+x22=5,與y軸的交點為C,它的頂點為M,求直線CM的表達式.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小穎和小強上山游玩,小穎乘坐纜車,小強步行,兩人相約在山頂的纜車終點會和,已知小強行走到纜車終點的路程是纜車到山頂的線路長的![]() 倍,小穎在小強出發后
倍,小穎在小強出發后![]() 分才乘上纜車,纜車的平均速度為
分才乘上纜車,纜車的平均速度為![]() 米/分,若圖中的折線表示小強在整個行走過程中的路程(米)與出發時間(分)之間的關系的圖像,請回答下列問題.
米/分,若圖中的折線表示小強在整個行走過程中的路程(米)與出發時間(分)之間的關系的圖像,請回答下列問題.

(1)小強行走的總路程是 米,他途中休息了 分;
(2)分別求出小強在休息前和休息后所走的兩段路程的速度;
(3)當小穎到達纜車終點時,小強離纜車終點的路程是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC中,AD是BC邊上的高,AE、BF分別是∠BAC、∠ABC的平分線,∠BAC=50°,∠ABC=60°,則∠EAD+∠ACD=( )

A. 75° B. 80° C. 85° D. 90°
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】推理填空:
如圖,![]() ,
,![]() ,將說明
,將說明![]() 成立的理由填寫完整.
成立的理由填寫完整.

解:因為![]() (已知),
(已知),
所以![]() (________________)
(________________)
又因為![]() (已知),
(已知),
所以![]() (等量代換),
(等量代換),
所以________________(同位角相等,兩直線平行),
所以![]() (________________________________)
(________________________________)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀材料:各類方程的解法
求解一元一次方程,根據等式的基本性質,把方程轉化為x=a的形式。求解二元一次方程組,把它轉化為一元一次方程來解:求解一元二次方程,把它轉化為兩個一元一次方程來解。求解分式方程,把它轉化為整式方程來解。各類方程的解法不盡相同,但是它們有一個共同的基本數學思想--轉化,把未知轉化為已知。
用“轉化”的數學思想,我們還可以解一些新的方程。例如,一元三次方程![]() ,可以通過因式分解把它轉化為
,可以通過因式分解把它轉化為![]() ,解方程
,解方程![]() 和
和![]() ,可得方程
,可得方程![]() 的解。
的解。
(1)問題:方程![]() 的解是
的解是![]() ,
,![]() _____,
_____,![]() _____。
_____。
(2)拓展:用“轉化”思想求方程![]() 的解。
的解。
(3)應用:如圖,已知矩形草坪ABCD的長![]() ,寬
,寬![]() ,小華把一根長為10m的繩子的一端固定在點B,沿草坪邊沿BA,AD走到點P處,把長繩PB段拉直并固定在點P,然后沿草坪邊沿PD、DC走到點C處,把長繩剩下的一段拉直,長繩的另一端恰好落在點C。求AP的長。
,小華把一根長為10m的繩子的一端固定在點B,沿草坪邊沿BA,AD走到點P處,把長繩PB段拉直并固定在點P,然后沿草坪邊沿PD、DC走到點C處,把長繩剩下的一段拉直,長繩的另一端恰好落在點C。求AP的長。
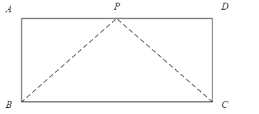
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com