【題目】若數a使得關于x的不等式組
，有且僅有四個整數解，且使關于y的分式方程
＝1有整數解，則所有滿足條件的整數a的值之和是（ ）
A. 3B. 2C. ﹣2D. ﹣3
【答案】A
【解析】
解關于x的不等式組
，根據“該不等式組有且僅有四個整數解”，得到關于a的不等式，解之，解分式方程
＝1，根據“該方程有整數解，且y≠﹣2”，得到a的取值范圍，結合a為整數，取所有符合題意的整數a，即可得到答案．
解：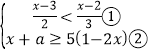
，
解不等式①得：x＜5，
解不等式②得：x
，
∵該不等式組有且僅有四個整數解，
∴該不等式組的解集為：
≤x＜5，
∴0＜≤1，
解得：﹣6≤a＜5，
＝1，
方程兩邊同時乘以（y+2）得：（a+4）﹣（2y+3）＝y+2，
去括號得：a+4﹣2y﹣3＝y+2，
移項得：﹣2y﹣y＝2+3﹣4﹣a，
合并同類項得：﹣3y＝1﹣a，
系數化為1得：y＝
，
∵該方程有整數解，且y≠﹣2，
a﹣1是3的整數倍，且a﹣1≠﹣6，
即a﹣1是3的整數倍，且a≠﹣5，
∵﹣6≤a＜5，
∴整數a為：﹣6，﹣5，﹣4，﹣3，﹣2，﹣1，0，1，2，3，4，
又∵即a﹣1是3的整數倍，且a≠﹣5，
∴a＝﹣2或a＝1或a＝4，
（﹣2）+1+4＝3，
故選：A．
各地期末復習特訓卷系列答案
小博士期末闖關100分系列答案科目：初中數學 來源： 題型：
【題目】已知在平面直角坐標系中，過點
向x軸作垂線，垂足為點M，點F從點M出發，沿x軸正方向以每秒1個單位長度的速度運動，連接AF，過點A作
交y軸于點E，設點F運動的時間是t秒
．
若點E在y軸的負半軸上
如圖所示
，求證：
；
如果點F運動時間是4秒．
求直線AE的表達式；
若直線AE與x軸的交點為B，C是y軸上一點，使
，求出C的坐標；
在點F運動過程中，設
，
，試用含m的代數式表示n．
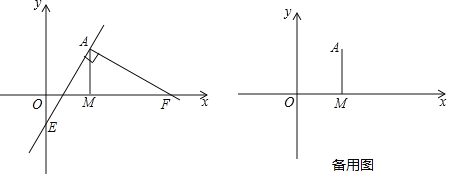
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，過點P（2，2
）作x軸的平行線交y軸于點A，交雙曲線y=
(x>0)于點N，作PM⊥AN交雙曲線y=(x>0)于點M，連接AM，若PN=4．
（1）求k的值；
（2）設直線MN解析式為y=ax+b，求不等式
ax+b的解集．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知反比例函數 
，下列結論中，不正確的是（ ）
A.圖象必經過點（1，2）
B.y隨x的增大而增大
C.圖象在第一、三象限內
D.若x＞1，則0＜y＜2
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，△ABC的三個頂點的坐標分別是A（3，3），B（1，1），C（4，–1）．
（1）直接寫出點A、B、C關于x軸對稱的點A1、B1、C1的坐標；A1（__________）、B1（__________）、C1（__________）．
（2）在圖中作出△ABC關于y軸對稱的圖形△A2B2C2．
（3）求△ABC的面積．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】若一個正整數a可以表示為連續的兩個奇數的平方差的形式，如：8＝32﹣12，16＝52﹣32，24＝72﹣52，……，我們則稱形如8，16，24這樣的正整數a為“奇特數”．
（1）請寫出最小的三位“奇特數”，并表示成連續的兩個奇數的平方差的形式；
（2）求證：任意一個“奇特數”都是8的倍數；
（3）若一個三位數b為“奇特數”，其百位和個位上的數字相同，十位上的數字比個位上的數字大m（m為正整數），求滿足條件的所有三位“奇特數”．
查看答案和解析>>
科目：初中數學 來源： 題型：
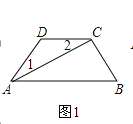
【題目】(1)如圖，AC平分∠DAB，∠1=∠2，試說明AB與CD的位置關系，并予以證明；
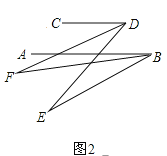
(2)如圖，AB∥CD，AB的下方兩點E、F滿足:BF平分∠ABE、DF平分∠CDE，若∠DFB=20°，∠CDE=70°，求∠ABE的度數；
(3)在前面的條件下，若P是BE上一點，G是CD上任一點，PQ平分∠BPG，PQ∥GN，GM平分∠DGP，下列結論:①∠DGP-∠MGN的值不變；②∠MGN的度數不變，可以證明只有一個是正確的，請你作出正確的選擇并求值.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知點A（0，0），B（2，0），點C在y軸上，且S△ABC＝3．
（1）求點C的坐標；
（2）以點A、B、C為頂點，作長方形，試寫出該長方形第四個頂點D的坐標．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
