Question

【題目】如圖，在Rt△ABC中，∠C=90°，AC=4，BC=3，AD為△ABC角平分線．
（1）用圓規在AB上作一點P，滿足DP⊥AB；
（2）求：CD的長度．

Answer 1

【答案】
（1）解：）、如圖，點P即為所求；

（2）解：∵AD平分∠BAC，

∴∠CAD=∠BAD．

又∵DC⊥AC、DP⊥AB，

∴∠C=∠APD．

在△ACD與APD中，

∵ ，

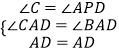∴△ACD≌APD（AAS）．

∴AP=AC=4，CD=PD．

在Rt△ABC中，∠C=90°，AC=4，BC=3，

∴AB=5．

設DP為x，則DP=x，BD=3﹣x，在Rt△DPB中，∠DPB=90°，

∴DP2+PB2=DB2，即，x2+12=（3﹣x）2，

解得x= ，

∴CD=DP= ．

【解析】（1）過點D作AB的垂線，垂足為P即可；（2）根據角平分線的性質可知∠CAD=∠BAD，利用AAS定理可知△ACD≌APD．在在Rt△ABC中根據勾股定理得出AB的長，設DP為x，則DP=x，BD=3﹣x，在Rt△DPB中，利用勾股定理即可得出結論．
【考點精析】解答此題的關鍵在于理解勾股定理的概念的相關知識，掌握直角三角形兩直角邊a、b的平方和等于斜邊c的平方,即;a2+b2=c2．