【題目】在數軸上，點A、B分別表示數a、b，且|a＋6|＋|b－10|＝0，記AB＝|a－b|
(1) 求AB的值
(2) 如圖，點P、Q分別從點A、B出發沿數軸向右運動，點P的速度是每秒4個單位長度，點Q的速度是每秒1個單位長度，點C從原點出發沿數軸向右運動，速度是每秒3個單位長度．經過多少秒，點C與點P、Q的距離相等？
(3) 在(2)的條件下，點M從對應－8的點出發沿數軸向左運動，速度是每秒4個單位長度，在運動過程中，MP＋MC－3MQ的值是否為定值？若是，求出其值，若不是，請說明理由
【答案】（1）16；（2）4；（3）是定值，為-44.
【解析】
（1）根據非負數的性質求得a、b的值，即可求得AB的值；（2）設設經過t秒，點C與點P、Q的距離相等，由題意可得方程6+3t-4t=10+t-3t，解方程即可求得t值；（3）是定值，設運動時間為t秒，則MP=4t+4t+2=8t+2，MC=4t+8+3t=7t+8，MQ=18+4t+t=18+5t，代入即可求得MP＋MC－3MQ的值.
（1）∵|a＋6|＋|b－10|＝0，
∴a=-6，b=10，
∴AB＝|a－b|=|-6-10|=16；
（2）設經過t秒，點C與點P、Q的距離相等，由題意可得，6+3t-4t=10+t-3t，
解得t=4；
答: 經過4秒，點C與點P、Q的距離相等；
（3）是定值，
設運動時間為t秒，則MP=4t+4t+2=8t+2，MC=4t+8+3t=7t+8，MQ=18+4t+t=18+5t，
∴MP＋MC－3MQ=8t+2+7t+8-3（18+5t）=15t+10-54-15t=-44.
新課標快樂提優暑假作業陜西旅游出版社系列答案科目：初中數學 來源： 題型：
【題目】（本題滿分8分）
為了加強學生課外閱讀，開闊視野，某校開展了“書香校園，從我做起”的主題活動．學校隨機抽取了部分學生，對他們一周的課外閱讀時間進行調查，繪制出頻數分布表和頻數分布直方圖的一部分如下：
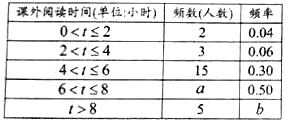
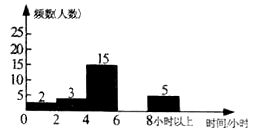
請根據圖表信息回答下列問題：
（1）頻數分布表中的
，
；
（2）將頻數分布直方圖補充完整；
（3）學校將每周課外閱讀時間在
小時以上的學生評為“閱讀之星”，請你估計該校
名學生中評為“閱讀之星”的有多少人？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知某開發區有一塊四邊形的空地ABCD，如圖所示，現計劃在空地上種植草皮，經測量∠A=90°，AB=3m，BC=12m，CD=13m，DA=4m，若每平方米草皮需要200元，問要多少投入？
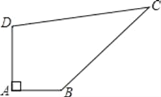
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】在有理數范圍內，我們定義三個數之間的新運算“
”法則：abc＝|a＋b＋c|－a＋b－c，例如：12(－3)＝|1＋2＋(－3)|－1＋2－(－3)＝4．在
這6個數中，任意取三個數作為a、b、c的值，則abc的最大值為___________
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】武漢市質量技術監督局從面粉廠生產的袋裝面粉中抽出20袋，檢測每袋的質量是否符合標準，把超過或不足的部分分別用正、負數來表示，記錄如下表：
與標準質量的差值（單位：克） | －6 | －2 | 0 | 1 | 3 | 4 |
袋數 | 1 | 4 | 3 | 4 | 5 | 3 |
(1) 若標準質量為450克，則抽出的20袋面粉的總質量為多少克？
(2) 若該包裝面粉的合格標準為450±3 克，求此次檢測的合格率
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖所示，在正方形ABCD中，點E是邊AB上一動點(不與A，B重合)，延長BA至點F，使AF=BE，連接CE，DF．
(1) 判斷四邊形CEFD的形狀，并說明理由；
(2) 如圖①，連接AC，過點E作EH⊥AC，垂足為點H．
①證明：AH=EH；
②若BE：AE=1：
，求∠BCE的度數；
③如圖②，連接FH，在點E的運動過程中，
的值是否發生變化？若不變，求出的值；若變化，請說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某校有3600名學生，為了解全校學生的上學方式，該校數學興趣小組以問卷調查的形式，隨機調查了該校部分學生的主要上學方式(參與問卷調查的學生只能從以下六個種類中選擇一類)，并將調查結果繪制成如下不完整的統計圖．
（1）參與本次問卷調查的學生共有 人，其中選擇D類的人數有 人；
（2）在扇形統計圖中，求E類對應的扇形圓心角
的度數，并補全C對應的條形統計圖；
（3）若將A、B、C．D．E這四類上學方式視為“綠色出行”，請估計該校選擇“綠色出行”的學生人數．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，
、
分別為數軸上的兩點，點對應的數為
，點對應的數為
．
（1）請寫出與、兩點距離相等的點
所對應的數；
（2）現有一只電子螞蟻
從點出發，以
單位/秒的速度向左運動，同時另一只電子螞蟻
恰好從點出發，以
單位/秒的速度向右運動，設兩只電子螞蟻在數軸上的
點相遇，你知道點對應的數是多少嗎？（寫出計算過程）
（3）在題（2）中，若運動t秒鐘時，兩只螞蟻的距離為10，求出t的值．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在平面直角坐標系中，拋物線y=ax2+4x+c與y軸交于點A（0，5），與x軸交于點E，B，點B坐標為（5，0）．
（1）求二次函數解析式及頂點坐標；
（2）過點A作AC平行于x軸，交拋物線于點C，點P為拋物線上的一點（點P在AC上方），作PD平行于y軸交AB于點D，問當點P在何位置時，四邊形APCD的面積最大？并求出最大面積．
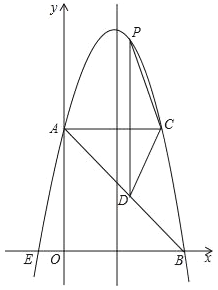
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com