
【題目】如圖,學校環保社成員想測量斜坡 ![]() 旁一棵樹
旁一棵樹 ![]() 的高度,他們先在點
的高度,他們先在點 ![]() 處測得樹頂
處測得樹頂 ![]() 的仰角為
的仰角為 ![]() ,然后在坡頂
,然后在坡頂 ![]() 測得樹頂
測得樹頂 ![]() 的仰角為
的仰角為 ![]() ,已知斜坡
,已知斜坡 ![]() 的長度為
的長度為 ![]() ,
, ![]() 的長為
的長為 ![]() ,則樹
,則樹 ![]() 的高度是( )
的高度是( ) ![]()
A.![]()
B.30
C.![]()
D.40
【答案】B
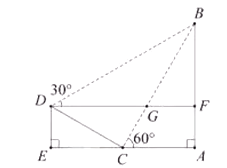
【解析】解:在Rt△DEC中,
∵CD=20,DE=10.
∴ ∠DCE=30°,∠CDE=60°.
∴ ∠CDF=30°.
又∵∠BDF=30°.∠BCA=60°.
∴ ∠BCD=30°.∠BDC=60°.
在Rt△BCD中,
∴ tan60°=![]() .
.
∴ BC=DCtan60°=20![]() .
.
在Rt△BAC中,
∴ sin60°=![]() .
.
∴ BA=BCsin60°=20![]() ×
×![]() =30(m).
=30(m).
故AB的高度為30m.
【考點精析】本題主要考查了解直角三角形的相關知識點,需要掌握解直角三角形的依據:①邊的關系a2+b2=c2;②角的關系:A+B=90°;③邊角關系:三角函數的定義.(注意:盡量避免使用中間數據和除法)才能正確解答此題.


 小學學習好幫手系列答案
小學學習好幫手系列答案 小學同步三練核心密卷系列答案
小學同步三練核心密卷系列答案科目:初中數學 來源: 題型:
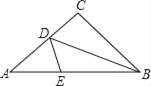
【題目】如圖,三角形紙牌中,AB=8cm,BC=6cm,AC=5cm,沿著過△ABC的頂點B的直線折疊這個三角形,使點C落在AB邊上的點E處,折痕為BD,則△AED周長為____.
查看答案和解析>>
科目:初中數學 來源: 題型:
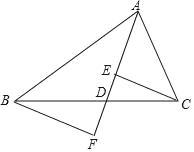
【題目】如圖,AD是△ABC的中線,E,F分別是AD和AD延長線上的點,且DE=DF,連接BF,CE,下列說法中正確的個數是( )
①CE=BF;②△ABD和△ADC的面積相等;③BF∥CE;④CE,BF均與AD垂直
A. 4個 B. 3個 C. 2個 D. 1個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】規定:四條邊對應相等,四個角對應相等的兩個四邊形全等.某學習小組在研究后發現判定兩個四邊形全等需要五組對應條件,于是把五組條件進行分類研究,并且針對二條邊和三個角對應相等類型進行研究提出以下幾種可能:
① AB=A1B1,AD=A1D1,∠A=∠A1,∠B=∠B1,∠C=∠C1;
② AB=A1B1,AD=A1D1,∠A=∠A1,∠B=∠B1,∠D=∠D1;
③ AB=A1B1,AD=A1D1,∠B=∠B1,∠C=∠C1,∠D=∠D1;
④ AB=A1B1,CD=C1D1,∠A=∠A1,∠B=∠B1,∠C=∠C1.
其中能判定四邊形ABCD和四邊形A1B1C1D1全等有( )個

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】郵遞員騎車從郵局出發,先向南騎行2km到達A村,繼續向南騎行3km到達B村,然后向北騎行9km到C村,最后回到郵局.
(1)以郵局為原點,以向北方向為正方向,用1cm表示1km,畫出數軸,并在該數軸上表示出A、B、C三個村莊的位置;
(2)C村離A村有多遠?
(3)郵遞員一共騎了多少千米?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】兩條直線都與第三條直線相交,∠1和∠2是內錯角,∠3和∠2是鄰補角.
(1)根據上述條件,畫出符合題意的圖形;
(2)若∠1∶∠2∶∠3=1∶2∶3,求∠1,∠2,∠3的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,拋物線y=ax2+bx+c與x軸交于點A(﹣1,0),B(4,0),與y軸交于點C(0,2),點D與點C關于x軸對稱,點P是x軸上的一個動點,設點P的坐標為(m,0),過點P作x軸的垂線l,交拋物線于點Q.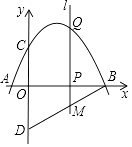
(1)求拋物線的解析式;
(2)求直線BD的解析式;
(3)當點P在線段OB上運動時,直線l交BD于點M,是否存在點P,使得四邊形CQMD是平行四邊形?若存在,求出m的值;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com