
【題目】正方形![]() 中,
中,![]() 為過頂點A的任意一條射線,過C作
為過頂點A的任意一條射線,過C作![]() 于E.
于E.

(1)若![]() ,
,![]() ,求
,求![]() 的長;
的長;
(2)過D作![]() 于F,過C作
于F,過C作![]() 于H,求證:
于H,求證:![]() .
.
【答案】(1)2![]() ;(2)見解析.
;(2)見解析.
【解析】
(1)根據正方形及勾股定理先求出AC的長度,再利用勾股定理,可求CE的長;
(2)證明△ADF≌△DCH,得到DF=CH,接著證明四邊形CEFH為矩形,從而有CH=EF,最后得到DF=EF.
(1)解:正方形ABCD中,AB=6,
∴BC=6,∠ABC=90°,∴AC=6![]() .
.
∵CE⊥AE,
∴CE=![]() ,
,
即CE=2![]() ;
;
(2)證明:∵CE⊥AE,DF⊥AE,CH⊥DF,
∴∠HFE=∠CHF=∠CEF=90°,
∴四邊形CEFH為矩形,
∴CH=EF,
∵∠ADH+∠HDC=∠HDC+∠DCH=90°,
∴∠ADH=∠DCH,
在△ADF和△DCH中,
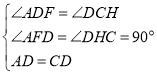 ,
,
∴△ADF≌△DCH(AAS),
∴DF=CH,
∴DF=EF.


科目:初中數學 來源: 題型:
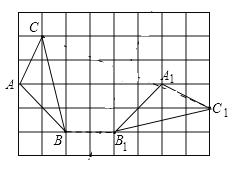
【題目】如圖,在邊長為1的小正方形組成的![]() 的方格中,
的方格中,![]() 和
和![]() 的頂點都在格點上,且
的頂點都在格點上,且![]() .利用平移、旋轉變換,能使
.利用平移、旋轉變換,能使![]() 通過一次或兩次變換后與
通過一次或兩次變換后與![]() 完全重合.
完全重合.
(1)請你寫出![]() 通過兩次變換與
通過兩次變換與![]() 完全重合的變換過程.
完全重合的變換過程.
(2)![]() 通過一次旋轉就能得到
通過一次旋轉就能得到![]() .請在圖中標出旋轉中心
.請在圖中標出旋轉中心![]() ,并簡要說明你是如何確定的.
,并簡要說明你是如何確定的.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AB是⊙O的直徑,AC與⊙O交于點D,點E在![]() 上,連接DE,AE,連接CE并延長交AB于點F,∠AED=∠ACF.
上,連接DE,AE,連接CE并延長交AB于點F,∠AED=∠ACF.
(1)求證:CF⊥AB;
(2)若CD=4,CB=4![]() ,cos∠ACF=
,cos∠ACF=![]() ,求EF的長.
,求EF的長.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】甲、乙兩個商場在同一周內經營同一種商品,每天的獲利情況如下表:
日期 | 星期一 | 星期二 | 星期三 | 星期四 | 星期五 | 星期六 | 星期天 |
甲商場獲利/萬元 | 2.5 | 2.4 | 2.8 | 3 | 3.2 | 3.5 | 3.6 |
乙商場獲利/萬元 | 1.9 | 2.3 | 2.7 | 2.6 | 3 | 4 | 4.5 |
(1)請你計算出這兩個商場在這周內每天獲利的平均數,并說明這兩個商場本周內總的獲利情況;
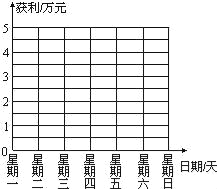
(2)在圖所示的網格圖內畫出兩個商場每天獲利的折線圖;(甲商場用虛線,乙商場用實線)
(3)根據折線圖,請你預測下周一哪個商場的獲利會多一些并簡單說出你的理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,CD∥AB,∠DCB=70°,∠CBF=20°,∠EFB=130°,
(1)問直線EF與AB有怎樣的位置關系?加以證明;
(2)若∠CEF=70°,求∠ACB的度數.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,平行四邊形![]() 的對角線
的對角線![]() 、
、![]() 相交于點O,
相交于點O,![]() .
.
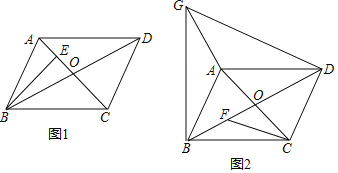
(1)如圖1,過B作![]() 于E,若
于E,若![]() ,
,![]() ,求
,求![]() 的長;
的長;
(2)如圖2,若![]() ,過點C作
,過點C作![]() 交
交![]() 于點F,過點B作
于點F,過點B作![]() 且
且![]() ,連接
,連接![]() .求證:
.求證:![]() .
.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,一次函數y=kx+b的圖象分別交x軸、y軸于A、B兩點,與反比例函數![]() 的圖象交于C、D兩點,DE⊥x軸于點E,已知C點的坐標是(6,﹣1),DE=3.
的圖象交于C、D兩點,DE⊥x軸于點E,已知C點的坐標是(6,﹣1),DE=3.

(1)求反比例函數與一次函數的解析式;
(2)求△CDE的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
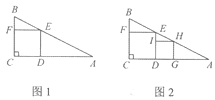
【題目】我們定義:“四個頂點都在三角形邊上的正方形是三角形的內接正方形”.已知:在Rt△ABC中,∠C=90°,AC=6,BC=3.
(1)如圖l,四邊形CDEF是△ABC的內接正方形,則正方形CDEF的邊長a1是________;
(2)如圖2,四邊形DGHI是(1)中△EDA的內接正方形,那么第2個正方形DGHI的邊長記為a2;繼續在圖2中的△HGA中按上述方法作第3個內接正方形……以此類推,則第n個內接正方形的邊長an=____. (n為正整數)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某市為提倡節約用水,準備實行自來水“階梯計費”方式,用戶用水不超出基本用水量的部分享受基本價格,超出基本用水量的部分實行超價收費,為更好的決策,自來水公司隨機抽取了部分用戶的用水量數據,并繪制了如圖不完整的統計圖,(每組數據包括在右端點但不包括左端點),請你根據統計圖解答下列問題:
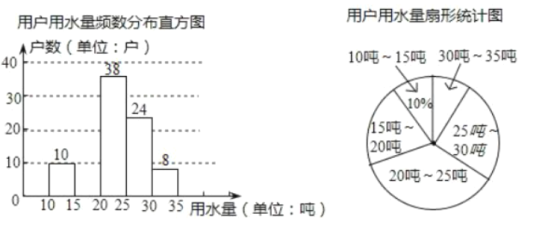
(1)此次抽樣調查的樣本容量是 .
(2)補全頻數分布直方圖,求扇形圖中“![]() 噸—
噸—![]() 噸”部分的圓心角的度數.
噸”部分的圓心角的度數.
(3)如果自來水公司將基本用水量定為每戶![]() 噸,那么該地區
噸,那么該地區![]() 萬用戶中約有多少用戶的用水全部享受基本價格?
萬用戶中約有多少用戶的用水全部享受基本價格?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com