
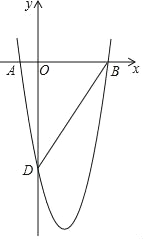
【題目】如圖,二次函數y=ax2+bx﹣4![]() 的圖象經過A(﹣1,0)、B(4,0)兩點,于y軸交于點D.
的圖象經過A(﹣1,0)、B(4,0)兩點,于y軸交于點D.
(1)求這個二次函數的表達式;
(2)已知點C(3,m)在這個二次函數的圖象上,連接BC,點P為拋物線上一點,且∠CBP=60°.
①求∠OBD的度數;
②求點P的坐標.
【答案】(1)二次函數的表達式為y=![]() x2﹣3
x2﹣3![]() x﹣4
x﹣4![]() ;(2)①60°,②(-
;(2)①60°,②(-![]() ,
,![]() )
)
【解析】分析:(1)代入A、B點坐標即可求得a、b的值,即可解題;
(2)①易證△BOD是含30°角的直角三角形,即可解題;
②過點P作PE⊥x軸于點E,過點C作CF⊥BD于點F,易證△CBF∽△PBE,可得![]() ,即可解題.
,即可解題.
詳解:(1)由題意知:![]() ,解得
,解得![]() .
.
∴該二次函數的表達式為y=![]() x2﹣3
x2﹣3![]() x﹣4
x﹣4![]() ;
;
(2)①∵當x=0時,y=﹣4![]() .
.
∴拋物線與y軸交點D的坐標為(0,﹣4![]() ).
).
∵在△BOD中,∠BOD=90°,OB=4,OD=4![]() ,
,
∴BD=![]() =8,即BD=2OB,
=8,即BD=2OB,
∴∠ODB=30°.
∴∠OBD=60°;
②過點P作PE⊥x軸于點E,過點C作CF⊥BD于點F,
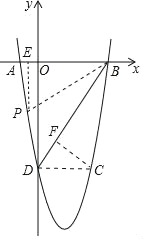
∵x=3時,m=﹣4![]() .
.
∴點C的坐標為(3,﹣4![]() ).
).
∵CD∥x軸,
∴CD=3,∠CDB=60°,∠DCF=30°.
∴DF=![]() CD=
CD=![]() ,CF=
,CF=![]() ,
,
∵BD=8,
∴BF=8﹣![]() =
=![]() ,
,
設點P的坐標為(x,![]() x2﹣3
x2﹣3![]() x﹣4
x﹣4![]() ).
).
則PE=﹣![]() x2+3
x2+3![]() x+4
x+4![]() ,BE=4﹣x,
,BE=4﹣x,
∵∠CBP=∠OBD=60°,
∴∠CBF=∠PBE.
∵∠CFB=∠PEB=90°.
∴△CBF∽△PBE.
∴![]() .
.
∴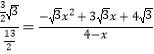 ,
,
解得:x1=4(舍去),x2=﹣![]() .
.
∵當x=﹣![]() 時,y=﹣
時,y=﹣![]() .
.
∴點P的坐標為(﹣![]() ,﹣
,﹣![]() ).
).


科目:初中數學 來源: 題型:
【題目】如圖,鐵路上A,B兩點相距25 km,C,D為兩村莊,DA⊥AB于點A,CB⊥AB于點B,已知DA=15 km,CB=10 km,現在要在鐵路AB上建一個土特產品收購站E,使得C,D兩村到E站的距離相等,則E站應建在離A站多少km處?

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】QQ運動記錄的小莉爸爸2017年2月份7天步行的步數(單位:萬步)如下表:
日期 | 2月6日 | 2月7日 | 2月8日 | 2月9日 | 2月10日 | 2月11日 | 2月12日 |
步數 | 2.1 | 1.7 | 1.8 | 1.9 | 2.0 | 1.8 | 2.0 |
(1)制作適當的統計圖表示小莉爸爸這7天步行的步數的變化趨勢;
(2)求小莉爸爸這7天中每天步行的平均步數;
(3)估計小莉爸爸2月份步行的總步數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,Rt△ABC的三個頂點分別是A(-4, 1),B(-1,3),C(-1,1)
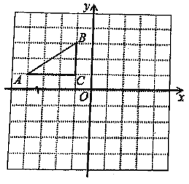
(1)將△ABC以原點O為旋轉中心旋轉180°,畫出旋轉后對應的△![]() ;平移△ABC,若A對應的點
;平移△ABC,若A對應的點![]() 坐標為(-4,-5),畫出△
坐標為(-4,-5),畫出△![]() ;
;
(2)若△![]() 繞某一點旋轉可以得到△
繞某一點旋轉可以得到△![]() ,直接寫出旋轉中心坐標是__________;
,直接寫出旋轉中心坐標是__________;
(3)在x軸上有一點P是的PA+PB的值最小,直接寫出點P的坐標___________;
查看答案和解析>>
科目:初中數學 來源: 題型:
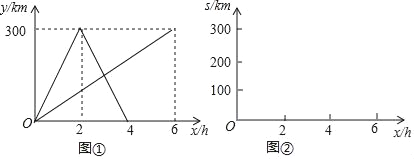
【題目】快車和慢車同時從甲地出發,勻速行駛,快車到達乙地后,原路返回甲地,慢車到達乙地停止.圖①表示兩車行駛過程中離甲地的路程y(km)與出發時間x(h)的函數圖象,請結合圖①中的信息,解答下列問題:
(1)快車的速度為 km/h,慢車的速度為 km/h,甲乙兩地的距離為 km;
(2)求出發多長時間,兩車相距100km;
(3)若兩車之間的距離為s km,在圖②的直角坐標系中畫出s(km)與x(h)的函數圖象.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知A、B兩地在數軸上相距20米,A地在數軸上表示的點為-8,小烏龜從A地出發沿數軸往B地方向前進,第一次前進1米,第二次后退2米,第三次再前進3米,第四次又后退4米,……,按此規律行進,(數軸的一個單位長度等于1米)
![]()
(1)求B地在數軸上表示的數;
(2)若B地在原點的左側,經過第五次行進后小烏龜到達點P,第六次行進后到達點Q,則點P和點Q到點A的距離相等嗎?請說明理由;
(3)若B地在原點的右側,那么經過30次行進后,小烏龜到達的點與點B之間的距離是多少米?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校對七、八、九年級的學生進行體育水平測試,成績評定為優秀、良好、合格、不合格四個等第.為了解這次測試情況,學校從三個年級隨機抽取200名學生的體育成績進行統計分析.相關數據的統計圖、表如下:
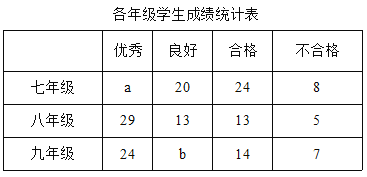

根據以上信息解決下列問題:
(1)在統計表中,a的值為 ,b的值為 ;
(2)在扇形統計圖中,八年級所對應的扇形圓心角為 度;
(3)若該校三個年級共有2000名學生參加考試,試估計該校學生體育成績不合格的人數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】我國是世界上嚴重缺水的國家之一.為了倡導“節約用水從我做起”,小剛在他所在班的50名同學中,隨機調查了10名同學家庭中一年的月均用水量(單位:t),并將調查結果繪成了如下的條形統計圖
【1】求這10個樣本數據的平均數、眾數和中位數;
【2】根據樣本數據,估計小剛所在班50名同學家庭中月均用水量不超過7 t的約有多少戶.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知數軸上的A、B兩點分別對應數字a、b,且a、b滿足|4a-b|+(a-4)2=0
![]()
(1)a= ,b= ,并在數軸上面出A、B兩點;
(2)若點P從點A出發,以每秒3個單位長度向x軸正半軸運動,求運動時間為多少時,點P到點A的距離是點P到點B距離的2倍;
(3)數軸上還有一點C的坐標為30,若點P和點Q同時從點A和點B出發,分別以每秒3個單位長度和每秒1個單位長度的速度向C點運動,P點到達C點后,再立刻以同樣的速度返回,運動到終點A.求點P和點Q運動多少秒時,P、Q兩點之間的距離為4,并求此時點Q對應的數.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com