
【題目】若整數a能被整數b整除,則一定存在整數n,使得![]() =n,即a=bn,例如:若整數a能被整數7整除,則一定存在整數n,使得
=n,即a=bn,例如:若整數a能被整數7整除,則一定存在整數n,使得![]() =n,即a=7n.
=n,即a=7n.
(1)將一個多位自然數分解為個位與個位之前的數,讓個位之前的數減去個位數的兩倍,若所得之差能被7整除,則原多位自然數一定能被7整除.例如:將數字1078分解為8和107,107﹣8×2=91,因為91能被7整除,所以1078能被7整除,請你證明任意一個三位數都滿足上述規律.
(2)若將一個多位自然數分解為個位與個位之前的數,讓個位之前的數加上個位數的k(k為正整數,1≤k≤15)倍,所得之和能被13整除,求當k為何值時使得原多位自然數一定能被13整除.
【答案】(1)見解析;(2)見解析
【解析】
試題分析:(1)根據題意設![]() ﹣2c=10a+b能被7整除,再假設
﹣2c=10a+b能被7整除,再假設![]() ﹣2c=7n( n為自然數 ),則10n+b=7n,進而表示出
﹣2c=7n( n為自然數 ),則10n+b=7n,進而表示出![]() ,即可得出答案;
,即可得出答案;
(2)首先設m+kn=13a,10m+n=13b,則原多位數為10m+n,進而得出b與a,k的關系,進而得出答案.
解:(1)設任意一個三位數為![]() (均為自然數且),
(均為自然數且),
依題意假設 ![]() ﹣2c=10a+b能被7整除,
﹣2c=10a+b能被7整除,
不妨設![]() ﹣2c=7n( n為自然數 ),則10n+b=7n,
﹣2c=7n( n為自然數 ),則10n+b=7n,
![]() =100a+10b+c=10(10a+b)+c=10(7n+2c)+c=7(10n+3c),
=100a+10b+c=10(10a+b)+c=10(7n+2c)+c=7(10n+3c),
所以 ![]() 能被7整除;
能被7整除;
(2)以下出現的字母均為自然數,設個位之前及個位數分別為m、n,
依題意不妨設m+kn=13a,
則原多位數為10m+n,
依題意不妨設10m+n=13b,
聯立可得:b=10a﹣![]() (10k﹣1),
(10k﹣1),
則10k﹣1為13倍數,分別將 k=1、2、3、4、5…15代入可知,只有k=4 時符合條件.


科目:初中數學 來源: 題型:
【題目】如圖,O為直線AB上一點,OD平分∠AOC,∠DOE=90°.
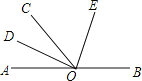
(1)若∠AOC=50°,求出∠BOD的度數;
(2)試判斷OE是否平分∠BOC,并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在正方形ABCD中,點A在y軸正半軸上,點B的坐標為(0,﹣3),反比例函數y=﹣![]() 的圖象經過點C.
的圖象經過點C.
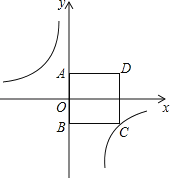
(1)求點C的坐標;
(2)若點P是反比例函數圖象上的一點且S△PAD=S正方形ABCD;求點P的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
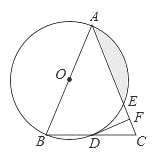
【題目】如圖,在△ABC中,AB=AC,以AB為直徑的⊙O分別與BC,AC交于點D,E,過點D作⊙O的切線DF,交AC于點F.
(1)求證:DF⊥AC;
(2)若⊙O的半徑為4,∠CDF=22.5°,求陰影部分的面積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com