
【題目】設(shè)數(shù)列![]() 是公差大于
是公差大于![]() 的等差數(shù)列,
的等差數(shù)列, ![]() 為數(shù)列
為數(shù)列![]() 的前
的前![]() 項(xiàng)和.已知
項(xiàng)和.已知![]() ,且
,且![]() 構(gòu)成等比數(shù)列.
構(gòu)成等比數(shù)列.
(1)求數(shù)列![]() 的通項(xiàng)公式;
的通項(xiàng)公式;
(2)若數(shù)列![]() 滿足
滿足![]() ,設(shè)
,設(shè)![]() 是數(shù)列
是數(shù)列![]() 的前
的前![]() 項(xiàng)和,證明:
項(xiàng)和,證明: ![]() .
.
【答案】(1)![]() ;(2)證明見解析.
;(2)證明見解析.
【解析】試題分析:(1)(1)利用等差數(shù)列前n項(xiàng)和、通項(xiàng)公式和等比數(shù)列,列出方程組,求出首項(xiàng)與公差,由此能求出數(shù)列{an}的通項(xiàng)公式.
(2)推導(dǎo)出bn=![]() =(2n-1)
=(2n-1) ![]() ,利用錯位相減法求出數(shù)列{bn}的前n項(xiàng)和,由此能證明Tn<6.
,利用錯位相減法求出數(shù)列{bn}的前n項(xiàng)和,由此能證明Tn<6.
試題解析:
(1)設(shè)數(shù)列{an}的公差為d,則d>0.
因?yàn)?/span>S3=9,所以a1+a2+a3=3a2=9,即a2=3.
因?yàn)?a1,a3-1,a4+1構(gòu)成等比數(shù)列,
所以(2+d)2=2(3-d)(4+2d),
所以d=2.所以an=a2+(n-2)d=2n-1.
(2)證明:因?yàn)?/span>![]() =2n-1(n∈N*),所以bn=
=2n-1(n∈N*),所以bn=![]() =(2n-1)
=(2n-1) ![]() ,
,
所以Tn=1×![]() +3×
+3×![]() +…+(2n-1)×
+…+(2n-1)×![]() ,①
,①
所以![]() Tn=1×
Tn=1×![]() +3×
+3×![]() +…+(2n-3)×
+…+(2n-3)×![]() +(2n-1)×
+(2n-1)×![]() ,②
,②
由①②兩式相減得![]() Tn=1+2×
Tn=1+2×![]() +2×
+2×![]() +…+2×
+…+2×![]() -(2n-1)×
-(2n-1)×![]() =1+
=1+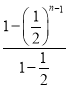 -
-![]() =3-
=3-![]() -
-![]() ,整理化簡得Tn=6-
,整理化簡得Tn=6-![]() .又因?yàn)?/span>n∈N*,所以Tn=6-
.又因?yàn)?/span>n∈N*,所以Tn=6-![]() <6.
<6.
點(diǎn)睛:用錯位相減法求和應(yīng)注意的問題:(1)要善于識別題目類型,特別是等比數(shù)列公比為負(fù)數(shù)的情形;(2)在寫出“Sn”與“qSn”的表達(dá)式時應(yīng)特別注意將兩式“錯項(xiàng)對齊”以便下一步準(zhǔn)確寫出“Sn-qSn”的表達(dá)式;(3)在應(yīng)用錯位相減法求和時,若等比數(shù)列的公比為參數(shù),應(yīng)分公比等于1和不等于1兩種情況求解.



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,矩形![]() 所在平面與半圓弧
所在平面與半圓弧![]() 所在平面垂直,
所在平面垂直,![]() 是
是![]() 上異于
上異于![]() ,
,![]() 的點(diǎn).
的點(diǎn).
(1)證明:平面![]() 平面
平面![]() ;
;
(2)在線段![]() 上是否存在點(diǎn)
上是否存在點(diǎn)![]() ,使得
,使得![]() 平面
平面![]() ?說明理由.
?說明理由.

查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某市為了制定合理的節(jié)水方案,對居民用水情況進(jìn)行了調(diào)查,通過抽樣,獲得了某年100位居民每人的月均用水量(單位:噸),將數(shù)據(jù)按照[0,0.5),[0.5,1),[4,4.5]分成9組,制成了如圖所示的頻率分布直方圖.
(I)求直方圖中的a值;
(II)設(shè)該市有30萬居民,估計(jì)全市居民中月均用水量不低于3噸的人數(shù),說明理由。

查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某研究所計(jì)劃利用“神舟十一號”飛船進(jìn)行新產(chǎn)品搭載實(shí)驗(yàn),計(jì)劃搭載新產(chǎn)品![]() ,要根據(jù)該產(chǎn)品的研制成本、產(chǎn)品質(zhì)量、搭載實(shí)驗(yàn)費(fèi)用和預(yù)計(jì)產(chǎn)生收益來決定具體安排,通過調(diào)查,搭載每件產(chǎn)品有關(guān)數(shù)據(jù)如表:
,要根據(jù)該產(chǎn)品的研制成本、產(chǎn)品質(zhì)量、搭載實(shí)驗(yàn)費(fèi)用和預(yù)計(jì)產(chǎn)生收益來決定具體安排,通過調(diào)查,搭載每件產(chǎn)品有關(guān)數(shù)據(jù)如表:
因素 | 產(chǎn)品 | 產(chǎn)品 | 備注 |
研制成本、搭載費(fèi)用之和/萬元 | 20 | 30 | 計(jì)劃最大投資 |
金額300萬元產(chǎn)品質(zhì)量/千克 | 10 | 5 | 最大搭載 |
質(zhì)量110千克預(yù)計(jì)收益/萬元 | 80 | 60 | —— |
則使總預(yù)計(jì)收益達(dá)到最大時, ![]() 兩種產(chǎn)品的搭載件數(shù)分別為( )
兩種產(chǎn)品的搭載件數(shù)分別為( )
A. 9,4 B. 8,5 C. 9,5 D. 8,4
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】從集合![]() 中任取三個不同的元素作為直線
中任取三個不同的元素作為直線![]() 中
中![]() 的值,若直線
的值,若直線![]() 傾斜角小于
傾斜角小于![]() ,且
,且![]() 在
在![]() 軸上的截距小于
軸上的截距小于![]() ,那么不同的直線
,那么不同的直線![]() 條數(shù)有( )
條數(shù)有( )
A. 109條B. 110條C. 111條D. 120條
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】研究發(fā)現(xiàn),北京 PM 2.5 的重要來源有土壤塵、燃煤、生物質(zhì)燃燒、汽車尾氣與垃圾焚燒、工業(yè)污染和二次無機(jī)氣溶膠,其中燃煤的平均貢獻(xiàn)占比約為 18%.為實(shí)現(xiàn)“節(jié)能減排”,還人民“碧水藍(lán)天”,北京市推行“煤改電”工程,采用空氣源熱泵作為冬天供暖.進(jìn)入冬季以來,該市居民用電量逐漸增加,為保證居民取暖,市供電部門對該市 100 戶居民冬季(按 120 天計(jì)算)取暖用電量(單位:度)進(jìn)行統(tǒng)計(jì)分析,得到居民冬季取暖用電量的頻率分布直方圖如圖所示.

(1)求頻率分布直方圖中![]() 的值;
的值;
(2)從這 100 戶居民中隨機(jī)抽取 1 戶進(jìn)行深度調(diào)查,求這戶居民冬季取暖用電量在[3300,3400]的概率;
(3)在用電量為[3200,3250),[3250,3300),[3300,3350),[3350,3400]的四組居民中,用分層抽樣的方法抽取 34 戶居民進(jìn)行調(diào)查,則應(yīng)從用電量在[3200,3250)的居民中抽取多少戶?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】下表數(shù)據(jù)為某地區(qū)某種農(nóng)產(chǎn)品的年產(chǎn)量![]() (單位:噸)及對應(yīng)銷售價格
(單位:噸)及對應(yīng)銷售價格![]() (單位:千元/噸).
(單位:千元/噸).
| 1 | 2 | 3 | 4 | 5 |
| 70 | 65 | 55 | 38 | 22 |
(1)若![]() 與
與![]() 有較強(qiáng)的線性相關(guān)關(guān)系,根據(jù)上表提供的數(shù)據(jù),用最小二乘法求出
有較強(qiáng)的線性相關(guān)關(guān)系,根據(jù)上表提供的數(shù)據(jù),用最小二乘法求出![]() 關(guān)于
關(guān)于![]() 的線性回歸方程;
的線性回歸方程;
(2)若該農(nóng)產(chǎn)品每噸的成本為13.1千元,假設(shè)該農(nóng)產(chǎn)品可全部賣出,利用上問所求的回歸方程,預(yù)測當(dāng)年產(chǎn)量為多少噸時,年利潤![]() 最大?
最大?
(參考公式:回歸直線方程為![]() ,其中
,其中 )
)
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在△ABC中,角A,B,C對應(yīng)的邊分別是a,b,c,已知cos2A﹣3cos(B+C)=1.
(1)求角A的大小;
(2)若△ABC的面積S=5![]() ,b=5,求sinBsinC的值.
,b=5,求sinBsinC的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】
在平面直角坐標(biāo)系![]() 中,直線
中,直線![]() 的參數(shù)方程為
的參數(shù)方程為![]() (
(![]() 為參數(shù),
為參數(shù), ![]() 為直線的傾斜角,且
為直線的傾斜角,且![]() ),以原點(diǎn)
),以原點(diǎn)![]() 為極點(diǎn),
為極點(diǎn), ![]() 軸的正半軸為極軸建立極坐標(biāo)系,圓
軸的正半軸為極軸建立極坐標(biāo)系,圓![]() 的極坐標(biāo)方程為
的極坐標(biāo)方程為![]() .
.
(1)若直線![]() 經(jīng)過圓
經(jīng)過圓![]() 的圓心,求直線
的圓心,求直線![]() 的傾斜角;
的傾斜角;
(2)若直線![]() 與圓
與圓![]() 交于
交于![]() ,
, ![]() 兩點(diǎn),且
兩點(diǎn),且![]() ,點(diǎn)
,點(diǎn)![]() ,求
,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com