
【題目】已知圓![]() ,直線
,直線![]()
(1)求證:直線![]() 過定點;
過定點;
(2)求直線![]() 被圓
被圓![]() 所截得的弦長最短時
所截得的弦長最短時![]() 的值;
的值;
(3)已知點![]() ,在直線MC上(C為圓心),存在定點N(異于點M),滿足:對于圓C上任一點P,都有
,在直線MC上(C為圓心),存在定點N(異于點M),滿足:對于圓C上任一點P,都有![]() 為一常數(shù),試求所有滿足條件的點N的坐標及該常數(shù).
為一常數(shù),試求所有滿足條件的點N的坐標及該常數(shù).

【答案】(1)直線![]() 過定點
過定點![]() (2)
(2)![]()
(3)在直線![]() 上存在定點
上存在定點![]() ,使得
,使得![]() 為常數(shù)
為常數(shù)![]()
【解析】分析:(Ⅰ)利用直線系方程的特征,直接求解直線l過定點A的坐標.
(Ⅱ)當AC⊥l時,所截得弦長最短,由題知![]() ,r=2,求出AC的斜率,利用點到直線的距離,轉化求解即可.
,r=2,求出AC的斜率,利用點到直線的距離,轉化求解即可.
(Ⅲ)由題知,直線MC的方程為![]() ,假設存在定點N
,假設存在定點N![]() 滿足題意,
滿足題意,
則設P(x,y),![]() ,得
,得![]()
![]() ,且
,且![]() ,求出λ,然后求解比值.
,求出λ,然后求解比值.
詳解:(Ⅰ)依題意得, ![]()
令![]() 且
且![]() ,得
,得![]()
![]() 直線
直線![]() 過定點
過定點![]()
(Ⅱ)當![]() 時,所截得弦長最短,由題知
時,所截得弦長最短,由題知![]() ,
, ![]()
![]()
![]() ,得
,得![]() ,
, ![]() 由
由![]() 得
得![]()
(Ⅲ)法一:由題知,直線![]() 的方程為
的方程為![]() ,假設存在定點
,假設存在定點![]() 滿足題意,
滿足題意,
則設![]() ,
, ![]() ,得
,得![]()
![]() ,且
,且![]()
![]()
![]()
整理得, ![]()
![]() 上式對任意
上式對任意![]() 恒成立,
恒成立, ![]()
![]() 且
且![]()
解得![]() ,說以
,說以![]() (舍去,與
(舍去,與![]() 重合),
重合),![]()
綜上可知,在直線![]() 上存在定點
上存在定點![]() ,使得
,使得![]() 為常數(shù)
為常數(shù)![]()


 名師指導期末沖刺卷系列答案
名師指導期末沖刺卷系列答案科目:高中數(shù)學 來源: 題型:
【題目】已知直線 ![]() 為參數(shù))經(jīng)過橢圓
為參數(shù))經(jīng)過橢圓 ![]() 為參數(shù))的左焦點
為參數(shù))的左焦點 ![]() .
.
(1)求 ![]() 的值;
的值;
(2)設直線 ![]() 與橢圓
與橢圓 ![]() 交于
交于 ![]() 兩點,求
兩點,求 ![]() 的最大值和最小值.
的最大值和最小值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖所示的莖葉圖記錄了甲、乙兩組各5名同學的投籃命中次數(shù),乙組記錄中有一個數(shù)據(jù)模糊,無法確認,在圖中用 ![]() 表示.
表示.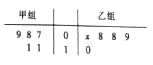
(1)若乙組同學投籃命中次數(shù)的平均數(shù)比甲組同學的平均數(shù)少1,求 ![]() 及乙組同學投籃命中次數(shù)的方差;
及乙組同學投籃命中次數(shù)的方差;
(2)在(1)的條件下,分別從甲、乙兩組投籃命中次數(shù)低于10次的同學中,各隨機選取一名,求這兩名同學的投籃命中次數(shù)之和為16的概率.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】在直角坐標系xOy中,曲線C1: ![]() (t為參數(shù),t ≠ 0),其中0 ≤ α < π,在以O為極點,x軸正半軸為極軸的極坐標系中,曲線C2:
(t為參數(shù),t ≠ 0),其中0 ≤ α < π,在以O為極點,x軸正半軸為極軸的極坐標系中,曲線C2: ![]() ,C3:
,C3: ![]() .
.
(1)求C2與C3交點的直角坐標;
(2)若C1與C2相交于點A,C1與C3相交于點B,求 ![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】學校藝術節(jié)對同一類的 ![]() ,
, ![]() ,
, ![]() ,
, ![]() 四項參賽作品,只評一項一等獎,在評獎揭曉前,甲、乙、丙、丁四位同學對這四項參賽作品預測如下:
四項參賽作品,只評一項一等獎,在評獎揭曉前,甲、乙、丙、丁四位同學對這四項參賽作品預測如下:
甲說:“是 ![]() 或
或 ![]() 作品獲得一等獎”;
作品獲得一等獎”;
乙說:“ ![]() 作品獲得一等獎”;
作品獲得一等獎”;
丙說:“ ![]() ,
, ![]() 兩項作品未獲得一等獎”;
兩項作品未獲得一等獎”;
丁說:“是 ![]() 作品獲得一等獎”.
作品獲得一等獎”.
若這四位同學中只有兩位說的話是對的,則獲得一等獎的作品是 .
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知 ![]() 展開式各項系數(shù)的和比它的二項式系數(shù)的和大992.
展開式各項系數(shù)的和比它的二項式系數(shù)的和大992.
(Ⅰ)求n;
(Ⅱ)求展開式中 ![]() 的項;
的項;
(Ⅲ)求展開式系數(shù)最大項.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】下列命題正確的個數(shù)為( )
①“x∈R都有x2≥0”的否定是“x0∈R使得x02≤0”;
②“x≠3”是“|x|≠3”成立的充分條件;
③命題“若m≤ ![]() ,則方程mx2+2x+2=0有實數(shù)根”的否命題為真命題.
,則方程mx2+2x+2=0有實數(shù)根”的否命題為真命題.
A.0
B.1
C.2
D.3
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】等差數(shù)列{an}的前n項和為Sn , 數(shù)列{bn}是等比數(shù)列,滿足a1=3,b1=1,b2+S2=10,a5﹣2b2=a3 .
(1)求數(shù)列{an}和{bn}的通項公式;
(2)令cn=anbn , 設數(shù)列{cn}的前n項和為Tn , 求Tn .
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】在如圖所示的多面體ABCDEF中,四邊形ABCD為正方形,底面ABFE為直角梯形,∠ABF為直角, ![]() , 平面ABCD⊥平面ABFE.
, 平面ABCD⊥平面ABFE.
(1)求證:DB⊥EC;
(2)若AE=AB,求二面角C﹣EF﹣B的余弦值.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com