
【題目】已知函數f(x)=ax﹣(a+2)lnx![]() 2,其中a∈R.
2,其中a∈R.
(1)當a=4時,求函數f(x)的極值;
(2)試討論函數f(x)在(1,e)上的零點個數.
【答案】(1)極大值6ln2,極小值4;(2)分類討論,詳見解析.
【解析】
(1)把a=4代入后對函數求導,然后結合導數可求函數的單調性,進而可求極值;
(2)先對函數求導,然后結合導數與單調性關系對a進行分類討論,確定導數符號,然后結合導數與函數的性質可求.
(1)當a=4時,f(x)=4x﹣6lnx![]() 2,
2,![]() ,x>0,
,x>0,
易得f(x)在(0,![]() ),(1,+∞)上單調遞增,在(
),(1,+∞)上單調遞增,在(![]() )上單調遞減,
)上單調遞減,
故當x![]() 時,函數取得極大值f(
時,函數取得極大值f(![]() )=6ln2,當x=1時,函數取得極小值f(1)=4,
)=6ln2,當x=1時,函數取得極小值f(1)=4,
(2)![]() ,
,
當a≤0時,f(x)在(1,e)上單調遞減,f(x)<f(1)=a≤0,此時函數在(1,e)上沒有零點;
當a≥2時,f(x)在(1,e)上單調遞增,f(x)>f(1)=a≥2,此時函數在(1,e)上沒有零點;
當0![]() 即
即![]() 時,f(x)在(1,e)上單調遞減,由題意可得,
時,f(x)在(1,e)上單調遞減,由題意可得, ,
,
解可得,0![]() ,
,
當![]() 即
即![]() 時,f(x)在(1,
時,f(x)在(1,![]() )上單調遞減,在(
)上單調遞減,在(![]() )上單調遞增,
)上單調遞增,
由于f(1)=a>0,f(e)=a(e﹣1)![]() ,
,
令g(a)=f(![]() )=2﹣(a+2)ln
)=2﹣(a+2)ln![]() a+2=(a+2)lna﹣(1+ln2)a+4﹣2ln2,
a+2=(a+2)lna﹣(1+ln2)a+4﹣2ln2,
令h(a)![]() ,則
,則![]() 0,
0,
所以h(a)在(![]() )上遞減,h(a)>h(2)=1>0,即g′(a)>0,
)上遞減,h(a)>h(2)=1>0,即g′(a)>0,
所以g(a)在(![]() )上遞增,g(a)>g(
)上遞增,g(a)>g(![]() )=2
)=2![]() ,
,
即f(![]() )>0,
)>0,
所以f(x)在(1,e)上沒有零點,
綜上,當0<a![]() 時,f(x)在(1,e)上有唯一零點,
時,f(x)在(1,e)上有唯一零點,
當a≤0或a![]() 時,f(x)在(1,e)上沒有零點.
時,f(x)在(1,e)上沒有零點.


科目:高中數學 來源: 題型:
【題目】為迎接“五一國際勞動節”,某商場規定購買超過6000元商品的顧客可以參與抽獎活動現有甲品牌和乙品牌的掃地機器人作為獎品,從這兩種品牌的掃地機器人中各隨機抽取6臺檢測它們充滿電后的工作時長相關數據見下表(工作時長單位:分)
機器序號 | 1 | 2 | 3 | 4 | 5 | 6 |
甲品牌工作時長/分 | 220 | 180 | 210 | 220 | 200 | 230 |
乙品牌工作時長/分 | 200 | 190 | 240 | 230 | 220 | 210 |
(1)根據所提供的數據,計算抽取的甲品牌的掃地機器人充滿電后工作時長的平均數與方差;
(2)從乙品牌被抽取的6臺掃地機器人中隨機抽出3臺掃地機器人,記抽出的掃地機器人充滿電后工作時長不低于220分鐘的臺數為![]() ,求
,求![]() 的分布列與數學期望.
的分布列與數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,橢圓![]() 的右頂點為
的右頂點為![]() ,左、右焦點分別為
,左、右焦點分別為![]() 、
、![]() ,過點
,過點![]() 且斜率為
且斜率為![]() 的直線與
的直線與![]() 軸交于點
軸交于點![]() ,與橢圓
,與橢圓![]() 交于另一個點
交于另一個點![]() ,且點
,且點![]() 在
在![]() 軸上的射影恰好為點
軸上的射影恰好為點![]() .
.
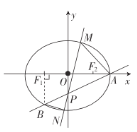
(1)求點![]() 的坐標;
的坐標;
(2)過點![]() 且斜率大于
且斜率大于![]() 的直線與橢圓交于
的直線與橢圓交于![]() 兩點
兩點![]() ,若
,若![]() ,求實數
,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
:![]() 過點
過點![]() ,過坐標原點
,過坐標原點![]() 作兩條互相垂直的射線與橢圓
作兩條互相垂直的射線與橢圓![]() 分別交于
分別交于![]() ,
,![]() 兩點.
兩點.
(1)證明:當![]() 取得最小值時,橢圓
取得最小值時,橢圓![]() 的離心率為
的離心率為![]() .
.
(2)若橢圓![]() 的焦距為2,是否存在定圓與直線
的焦距為2,是否存在定圓與直線![]() 總相切?若存在,求定圓的方程;若不存在,請說明理由.
總相切?若存在,求定圓的方程;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=sin(ωx+φ)(ω>0,![]() )的最小正周期為π,且關于
)的最小正周期為π,且關于![]() 中心對稱,則下列結論正確的是( )
中心對稱,則下列結論正確的是( )
A.f(1)<f(0)<f(2)B.f(0)<f(2)<f(1)
C.f(2)<f(0)<f(1)D.f(2)<f(1)<f(0)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設拋物線![]() 的焦點為
的焦點為![]() ,直線
,直線![]() 與拋物線交于
與拋物線交于![]() 兩點.
兩點.
(1)若![]() 過點
過點![]() ,且
,且![]() ,求
,求![]() 的斜率;
的斜率;
(2)若![]() ,且
,且![]() 的斜率為
的斜率為![]() ,當
,當![]() 時,求
時,求![]() 在
在![]() 軸上的截距的取值范圍(用
軸上的截距的取值范圍(用![]() 表示),并證明
表示),并證明![]() 的平分線始終與
的平分線始終與![]() 軸平行.
軸平行.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若數列![]() 滿足
滿足![]() ,數列
,數列![]() 為
為![]() 數列,記
數列,記![]() .
.
(1)寫出一個滿足![]() ,且
,且![]() 的
的![]() 數列
數列![]() ;
;
(2)若![]() ,
,![]() ,證明:
,證明:![]() 數列
數列![]() 是遞增數列的充要條件是
是遞增數列的充要條件是![]() ;
;
(3)對任意給定的整數![]() ,是否存在首項為0的
,是否存在首項為0的![]() 數列
數列![]() ,使得
,使得![]() ?如果存在,寫出一個滿足條件的
?如果存在,寫出一個滿足條件的![]() 數列
數列![]() ;如果不存在,說明理由.
;如果不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】趙爽是我國漢代數學家、天文學家,他在注解《周髀算經》時,介紹了“勾股圓方圖”,亦稱“趙爽弦圖”,它被2002年國際數學家大會選定為會徽.“趙爽弦圖”是以弦為邊長得到的正方形,該正方形由4個全等的直角三角形加上中間一個小正方形組成類比“趙爽弦圖”,可類似地構造如圖所示的圖形它是由3個全等的三角形與中間的一個小等邊三角形拼成的一個大等邊三角形設DF=2AF=2,若在大等邊三角形中隨機取一點,則此點取自三個全等三角形(陰影部分)的概率是( )
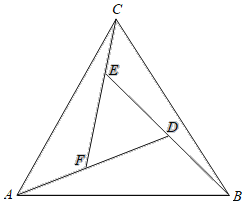
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com