
【題目】現有正方形ABCD和一個以O為直角頂點的三角板,移動三角板,使三角板兩直角邊所在直線分別與直線BC、CD交于點M、N.
(1)如圖1,若點O與點A重合,則OM與ON的數量關系是
(2)如圖2,若點O在正方形的中心(即兩對角線交點),則(1)中的結論是否仍然成立?請說明理由;
(3)如圖3,若點O在正方形的內部(含邊界),當OM=ON時,請探究點O在移動過程中可形成什么圖形?
(4)如圖4,是點O在正方形外部的一種情況.當OM=ON時,請你就“點O的位置在各種情況下(含外部)移動所形成的圖形”提出一個正確的結論.(不必說明)
【答案】
(1)OM=ON
(2)
解:仍成立.
證明:如圖2,

連接AC、BD,則
由正方形ABCD可得,∠BOC=90°,BO=CO,∠OBM=∠OCN=45°
∵∠MON=90°
∴∠BOM=∠CON
在△BOM和△CON中

∴△BOM≌△CON(ASA)
∴OM=ON.
(3)
解:如圖3,

過點O作OE⊥BC,作OF⊥CD,垂足分別為E、F,則∠OEM=∠OFN=90°
又∵∠C=90°
∴∠EOF=90°=∠MON
∴∠MOE=∠NOF
在△MOE和△NOF中

∴△MOE≌△NOF(AAS)
∴OE=OF
又∵OE⊥BC,OF⊥CD
∴點O在∠C的平分線上
∴O在移動過程中可形成線段AC.
(4)
解:O在移動過程中可形成直線AC.

【解析】(1)解:若點O與點A重合,則OM與ON的數量關系是:OM=ON;
(1)根據△OBM與△ODN全等,可以得出OM與ON相等的數量關系;
(2)連接AC、BD,則通過判定△BOM≌△CON,可以得到OM=ON;
(3)過點O作OE⊥BC,作OF⊥CD,可以通過判定△MOE≌△NOF,得出OE=OF,進而發現點O在∠C的平分線上;
(4)可以運用(3)中作輔助線的方法,判定三角形全等并得出結論.本題主要考查了四邊形中的正方形,解決問題的關鍵是作輔助線構造全等三角形.解題時需要運用全等三角形的判定與性質,以及角平分線的判定定理.


科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
已知曲線![]() 的極坐標方程為
的極坐標方程為![]() ,以極點為原點,極軸為
,以極點為原點,極軸為![]() 軸的正半軸,建立平面直角坐標系,直線
軸的正半軸,建立平面直角坐標系,直線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數).
為參數).
(1)判斷直線![]() 與曲線
與曲線![]() 的位置關系,并說明理由;
的位置關系,并說明理由;
(2)若直線![]() 和曲線
和曲線![]() 相交于
相交于![]() 兩點,且
兩點,且![]() ,求直線
,求直線![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知四邊形ABCD為正方形,PD⊥平面ABCD且PD=AD,則下列命題中錯誤的是( )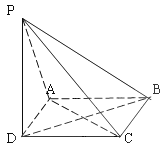
A.過BD且與PC平行的平面交PA于M點,則M為PA的中點
B.過AC且與PB垂直的平面交PB于N點,則N為PB的中點
C.過AD且與PC垂直的平面交PC于H點,則H為PC的中點
D.過P、B、C的平面與平面PAD的交線為直線l,則l∥AD
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在△ABC中,AB=AC=5,BC=8,D是線段BC上的動點(不含端點B、C).若線段AD長為正整數,則點D的個數共有( )
A.5個
B.4個
C.3個
D.2個
查看答案和解析>>
科目:高中數學 來源: 題型:
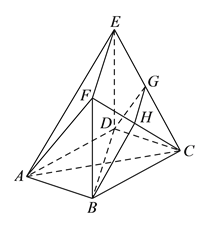
【題目】如圖,在多面體![]() 中,底面
中,底面![]() 是邊長為
是邊長為![]() 的正方形,四邊形
的正方形,四邊形![]() 是矩形,平面
是矩形,平面![]() 平面
平面![]() ,
, ![]() ,
, ![]() 和
和![]() 分別是
分別是![]() 和
和![]() 的中點.
的中點.
(Ⅰ)求證: ![]() 平面
平面![]() .
.
(Ⅱ)求證:平面![]() 平面
平面![]() .
.
(Ⅲ)求多面體![]() 的體積.
的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知雙曲線![]() 的焦點是橢圓
的焦點是橢圓![]() :
: ![]() (
(![]() )的頂點,且橢圓與雙曲線的離心率互為倒數.
)的頂點,且橢圓與雙曲線的離心率互為倒數.
(Ⅰ)求橢圓![]() 的方程;
的方程;
(Ⅱ)設動點![]() ,
, ![]() 在橢圓
在橢圓![]() 上,且
上,且![]() ,記直線
,記直線![]() 在
在![]() 軸上的截距為
軸上的截距為![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某企業為了解下屬某部門對本企業職工的服務情況,隨機訪問50名職工,根據這50名職工對該部門的評分,繪制頻率分布直方圖(如圖所示),其中樣本數據分組區間為![]()

(1)求頻率分布直方圖中![]() 的值;
的值;
(2)估計該企業的職工對該部門評分不低于80的概率;
(3)從評分在![]() 的受訪職工中,隨機抽取2人,求此2人評分都在
的受訪職工中,隨機抽取2人,求此2人評分都在![]() 的概率.
的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com