
【題目】某險種的基本保費(fèi)為![]() (單位:元),繼續(xù)購買該險種的投保人稱為續(xù)保人,續(xù)保人本年度的保費(fèi)與其
(單位:元),繼續(xù)購買該險種的投保人稱為續(xù)保人,續(xù)保人本年度的保費(fèi)與其
上年度出險次數(shù)的關(guān)聯(lián)如下:
上年度出險次數(shù) | 0 | 1 | 2 | 3 | 4 |
|
保費(fèi) |
|
|
|
|
|
|
隨機(jī)調(diào)查了該險種的200名續(xù)保人在一年內(nèi)的出險情況,得到如下統(tǒng)計表:
出險次數(shù) | 0 | 1 | 2 | 3 | 4 |
|
頻數(shù) | 60 | 50 | 30 | 30 | 20 | 10 |
(1)記A為事件:“一續(xù)保人本年度的保費(fèi)不高于基本保費(fèi)”.求![]() 的估計值;
的估計值;
(2)記B為事件:“一續(xù)保人本年度的保費(fèi)高于基本保費(fèi)但不高于基本保費(fèi)的160%”.求![]() 的估計值;
的估計值;
【答案】(1)0.55;(2)0.3.
【解析】
(1)求出![]() 為事件:“一續(xù)保人本年度的保費(fèi)不高于基本保費(fèi)”的人數(shù).即可求
為事件:“一續(xù)保人本年度的保費(fèi)不高于基本保費(fèi)”的人數(shù).即可求![]() 的估計值;
的估計值;
(2)求出![]() 為事件:“一續(xù)保人本年度的保費(fèi)高于基本保費(fèi)但不高于基本保費(fèi)的160%”的人數(shù).然后求
為事件:“一續(xù)保人本年度的保費(fèi)高于基本保費(fèi)但不高于基本保費(fèi)的160%”的人數(shù).然后求![]() 的估計值;
的估計值;
(1)事件A發(fā)生當(dāng)且僅當(dāng)一年內(nèi)出險次數(shù)小于2,由所給數(shù)據(jù)知,一年內(nèi)險次數(shù)小于2的頻率為![]() ,
,
所以![]() 的估計值為
的估計值為![]()
(2)事件B發(fā)生當(dāng)且僅當(dāng)一年內(nèi)出險次數(shù)大于1且小于4.由是給數(shù)據(jù)知,一年內(nèi)出險次數(shù)大于1且小于4的頻率為![]() ,
,
故P(B)的估計值為0.3.


 99加1領(lǐng)先期末特訓(xùn)卷系列答案
99加1領(lǐng)先期末特訓(xùn)卷系列答案 百強(qiáng)名校期末沖刺100分系列答案
百強(qiáng)名校期末沖刺100分系列答案 好成績1加1期末沖刺100分系列答案
好成績1加1期末沖刺100分系列答案 金狀元績優(yōu)好卷系列答案
金狀元績優(yōu)好卷系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() ,曲線
,曲線![]() 在點(diǎn)
在點(diǎn)![]() 處的切線平行于
處的切線平行于![]() 軸.
軸.
(1)求![]() 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(2)證明:當(dāng)![]() 時,
時,![]() 恒成立.
恒成立.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】因市場戰(zhàn)略儲備的需要,某公司![]() 月
月![]() 日起,每月
日起,每月![]() 日購買了相同金額的某種物資,連續(xù)購買了
日購買了相同金額的某種物資,連續(xù)購買了![]() 次.由于市場變化,
次.由于市場變化,![]() 月
月![]() 日該公司不得不將此物資全部賣出.已知該物資的購買和賣出都是以份為計價單位進(jìn)行交易,且該公司在買賣的過程中沒有虧本,那么下面
日該公司不得不將此物資全部賣出.已知該物資的購買和賣出都是以份為計價單位進(jìn)行交易,且該公司在買賣的過程中沒有虧本,那么下面![]() 個折線圖中,所有可以反映這種物資每份價格(單位:萬元)的變化情況的是( )
個折線圖中,所有可以反映這種物資每份價格(單位:萬元)的變化情況的是( )

A.①②B.①③C.②③D.③
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() ,
,![]() .
.
(1)若函數(shù)![]() 在定義域內(nèi)單調(diào)遞增,求實數(shù)
在定義域內(nèi)單調(diào)遞增,求實數(shù)![]() 的取值范圍;
的取值范圍;
(2)證明:方程![]() 有且只有一個實數(shù)根.
有且只有一個實數(shù)根.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
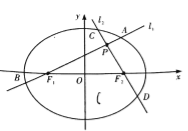
【題目】如圖,分別過橢圓![]() 左、右焦點(diǎn)
左、右焦點(diǎn)![]() 的動直線
的動直線![]() 相交于
相交于![]() 點(diǎn),與橢圓
點(diǎn),與橢圓![]() 分別交于
分別交于![]() 與
與![]() 不同四點(diǎn),直線
不同四點(diǎn),直線![]() 的斜率
的斜率![]() 滿足
滿足![]() , 已知
, 已知![]() 與
與![]() 軸重合時,
軸重合時, ![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)是否存在定點(diǎn)![]() 使得
使得![]() 為定值,若存在,求出
為定值,若存在,求出![]() 點(diǎn)坐標(biāo)并求出此定值,若不存在,
點(diǎn)坐標(biāo)并求出此定值,若不存在,
說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】若函數(shù)![]() 同時滿足:⑴對于定義域上的任意
同時滿足:⑴對于定義域上的任意![]() ,恒有
,恒有![]() ; ⑵對于定義域上的任意
; ⑵對于定義域上的任意![]() ,當(dāng)
,當(dāng)![]() 時,恒有
時,恒有![]() ,則稱函數(shù)
,則稱函數(shù)![]() 為“理想函數(shù)”.給出下列四個函數(shù)中: ①
為“理想函數(shù)”.給出下列四個函數(shù)中: ①![]() ,②
,②![]() , ③
, ③![]() ,④
,④ ,能被稱為“理想函數(shù)”的有_____________(填相應(yīng)的序號).
,能被稱為“理想函數(shù)”的有_____________(填相應(yīng)的序號).
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】從某小學(xué)隨機(jī)抽取100名同學(xué),將他們的身高(單位:厘米)數(shù)據(jù)繪制成頻率分布直方圖(如下圖).由圖中數(shù)據(jù)可知a=________,估計該小學(xué)學(xué)生身高的中位數(shù)為______

查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在四棱錐![]() 中,
中,![]() 底面
底面![]() ,
,![]() ,
,![]() ,
,![]() ,點(diǎn)
,點(diǎn)![]() 為棱
為棱![]() 的中點(diǎn),
的中點(diǎn),

(1)證明:![]() ;
;
(2)若點(diǎn)![]() 為棱
為棱![]() 上一點(diǎn),且
上一點(diǎn),且![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】函數(shù)![]() 的部分圖像如圖所示,將
的部分圖像如圖所示,將![]() 的圖象向右平移
的圖象向右平移![]() 個單位長度后得到函數(shù)
個單位長度后得到函數(shù)![]() 的圖象.
的圖象.

(1)求函數(shù)![]() 的解析式;
的解析式;
(2)在![]() 中,角A,B,C滿足
中,角A,B,C滿足![]() ,且其外接圓的半徑R=2,求
,且其外接圓的半徑R=2,求![]() 的面積的最大值.
的面積的最大值.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com