
【題目】已知函數(shù)f(x)=ex﹣![]() 有兩個極值點.
有兩個極值點.
(1)求實數(shù)a的取值范圍;
(2)若函數(shù)f(x)的兩個極值點分別為x1,x2,求證:x1+x2>2.
【答案】(1)(e,+∞);(2)見解析
【解析】
(1)f′(x)=ex﹣ax.函數(shù)f(x)=ex![]() 有兩個極值點f′(x)=ex﹣ax=0有兩個實數(shù)根.x=0時不滿足上述方程,方程化為:a
有兩個極值點f′(x)=ex﹣ax=0有兩個實數(shù)根.x=0時不滿足上述方程,方程化為:a![]() ,令g(x)
,令g(x)![]() ,(x≠0).利用導數(shù)已經(jīng)其單調性即可得出.
,(x≠0).利用導數(shù)已經(jīng)其單調性即可得出.
(2)由(1)可知:a>e時,函數(shù)f(x)有兩個極值點分別為![]() ,x2,不妨設
,x2,不妨設![]() <
<![]() ,
,![]() +
+![]() >2
>2![]() >2﹣
>2﹣![]() >1
>1![]() ,由
,由![]() ,因此即證明:
,因此即證明:![]() .構造函數(shù)h(x)
.構造函數(shù)h(x)![]() ,0<x<1,2﹣x>1.利用導數(shù)已經(jīng)其單調性即可得出.
,0<x<1,2﹣x>1.利用導數(shù)已經(jīng)其單調性即可得出.
(1)解:f′(x)=ex﹣ax.
∵函數(shù)f(x)=ex![]() 有兩個極值點.
有兩個極值點.
∴f′(x)=ex﹣ax=0有兩個實數(shù)根.
x=0時不滿足上述方程,
方程化為:a![]() ,
,
令g(x)![]() ,(x≠0).
,(x≠0).
g′(x)![]() ,
,
可得:x<0時,g′(x)<0,函數(shù)g(x)單調遞減;0<x<1時,g′(x)<0,函數(shù)g(x)單調遞減;x>1時,g′(x)>0,函數(shù)g(x)單調遞增.
g(1)=e,得到函數(shù)草圖如圖所示.
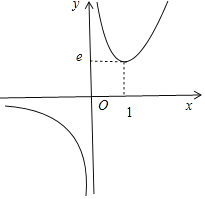
a>e時,方程f′(x)=ex﹣ax=0有兩個實數(shù)根.
∴實數(shù)a的取值范圍是(e,+∞).
(2)證明:由(1)可知:a>e時,函數(shù)f(x)有兩個極值點分別為x1,x2,不妨設x1<x2.
證明:![]() +
+![]() >2
>2![]() >2﹣
>2﹣![]() >1
>1![]() ,
,
由![]() ,因此即證明:
,因此即證明:![]() .
.
構造函數(shù)h(x)![]() ,0<x<1,2﹣x>1.
,0<x<1,2﹣x>1.
h′(x)![]() (x﹣1)
(x﹣1)![]() ,
,
令函數(shù)u(x)![]() ,(0<x<2).
,(0<x<2).
u′(x)![]() .
.
可得函數(shù)u(x)在(0,2)內單調遞減,于是函數(shù)v(x)![]() 在(0,1)內單調遞減.
在(0,1)內單調遞減.
v(x)≥v(1)=0.∴h′(x)![]() (x﹣1)
(x﹣1)![]() ,h(x)在(0,1)內單調遞減.
,h(x)在(0,1)內單調遞減.
∴h(x)>h(1)=0,
∴![]() .
.
因此![]() +
+![]() >2成立.
>2成立.


科目:高中數(shù)學 來源: 題型:
【題目】設F1,F2分別是橢圓![]() 的左、右焦點,過
的左、右焦點,過![]() 的直線
的直線![]() 與
與![]() 相交 于A,B兩點,且|AF2|,|AB|,|BF2|成等差數(shù)列.
相交 于A,B兩點,且|AF2|,|AB|,|BF2|成等差數(shù)列.
(1)求|AB|;
(2)若直線![]() 的斜率為1,求實數(shù)
的斜率為1,求實數(shù)![]() 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如果對定義在R上的奇函數(shù)y=f(x),對任意兩個不相鄰的實數(shù)x1,x2,所有x1f(x1)+x2f(x2)>x1f(x2)+x2f(x1),則稱函數(shù)y=f(x)為“H函數(shù)”,下列函數(shù)為H函數(shù)的是( )
A. f(x)=sinxB. f(x)=exC. f(x)=x3﹣3xD. f(x)=x|x|
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
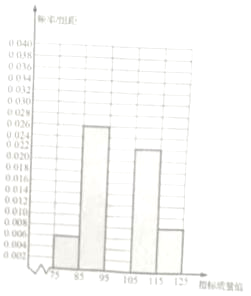
【題目】從某企業(yè)生產(chǎn)的某種產(chǎn)品中抽取100件,測量這些產(chǎn)品的一項質量指標值.由測量表得到如下頻率分布直方圖
(1)補全上面的頻率分布直方圖(用陰影表示);
(2)統(tǒng)計方法中,同一組數(shù)據(jù)常用該組區(qū)間的中間值作為代表,據(jù)此估計這種產(chǎn)品質量指標值服從正態(tài)分布Z(μ,σ2),其中μ近似為樣本平均值![]() ,σ2近似為樣本方差s2(組數(shù)據(jù)取中間值);
,σ2近似為樣本方差s2(組數(shù)據(jù)取中間值);
①利用該正態(tài)分布,求從該廠生產(chǎn)的產(chǎn)品中任取一件,該產(chǎn)品為合格品的概率;
②該企業(yè)每年生產(chǎn)這種產(chǎn)品10萬件,生產(chǎn)一件合格品利潤10元,生產(chǎn)一件不合格品虧損20元,則該企業(yè)的年利潤是多少?
參考數(shù)據(jù):![]() =5.1,若Z~N(μ,σ2),則P(μ﹣σ,μ+σ)=0.6826,P(μ﹣2σ,μ+2σ)=0.9544.
=5.1,若Z~N(μ,σ2),則P(μ﹣σ,μ+σ)=0.6826,P(μ﹣2σ,μ+2σ)=0.9544.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
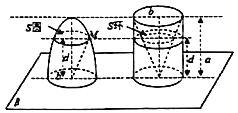
【題目】我國齊梁時代的數(shù)學家祖暅提出了一條原理:“冪勢既同,則積不容異”.意思是:兩個等高的幾何體若在所有等高處的水平截面的面積相等,則這兩個幾何體的體積相等.橢球體是橢圓繞其軸旋轉所成的旋轉體.如圖,將底面直徑都為![]() ,高皆為
,高皆為![]() 的橢半球體和已被挖去了圓錐體的圓柱放置于同一平面
的橢半球體和已被挖去了圓錐體的圓柱放置于同一平面![]() 上,用平行于平面
上,用平行于平面![]() 且與平面
且與平面![]() 任意距離
任意距離![]() 處的平面截這兩個幾何體,可橫截得到
處的平面截這兩個幾何體,可橫截得到![]() 及
及![]() 兩截面.可以證明
兩截面.可以證明![]() 總成立.據(jù)此,半短軸長為1,半長軸長為3的橢球體的體積是_______.
總成立.據(jù)此,半短軸長為1,半長軸長為3的橢球體的體積是_______.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】設集合A={x|x2-3x+2=0},B={x|x2+(a-1)x+a2-5=0}.
(1)若A∩B={2},求實數(shù)a的值;
(2)若A∪B=A,求實數(shù)a的取值范圍.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com