
【題目】設a>0, ![]() 是R上的偶函數.
是R上的偶函數.
(1)求a的值;
(2)證明:f(x)在(0,+∞)上是增函數.
【答案】
(1)解:∵a>0, ![]() 是R上的偶函數.
是R上的偶函數.
∴f(﹣x)=f(x),即 ![]() +
+ ![]() =
= ![]() ,
,
∴ ![]() +a2x=
+a2x= ![]() +
+ ![]() ,
,
2x(a﹣ ![]() )﹣
)﹣ ![]() (a﹣
(a﹣ ![]() )=0,
)=0,
∴(a﹣ ![]() )(2x+
)(2x+ ![]() )=0,∵2x+
)=0,∵2x+ ![]() >0,a>0,
>0,a>0,
∴a﹣ ![]() =0,解得a=1,或a=﹣1(舍去),
=0,解得a=1,或a=﹣1(舍去),
∴a=1;
(2)證明:由(1)可知 ![]() ,
,
∴ ![]()
∵x>0,
∴22x>1,
∴f'(x)>0,
∴f(x)在(0,+∞)上單調遞增
【解析】(1)根據偶函數的性質f(﹣x)=f(x),代入即可求出a的值;(2)由(1)求出了f(x)的解析式,對f(x)進行求導,證明其導數大于0即可;
【考點精析】本題主要考查了函數單調性的判斷方法和函數奇偶性的性質的相關知識點,需要掌握單調性的判定法:①設x1,x2是所研究區間內任兩個自變量,且x1<x2;②判定f(x1)與f(x2)的大小;③作差比較或作商比較;在公共定義域內,偶函數的加減乘除仍為偶函數;奇函數的加減仍為奇函數;奇數個奇函數的乘除認為奇函數;偶數個奇函數的乘除為偶函數;一奇一偶的乘積是奇函數;復合函數的奇偶性:一個為偶就為偶,兩個為奇才為奇才能正確解答此題.


科目:高中數學 來源: 題型:
【題目】解答題
(1)設p:實數x滿足(x﹣3a)(x﹣a)<0,其中a>0,q:實數x滿足 ![]() ,若p是q的充分不必要條件,求實數a的取值范圍;
,若p是q的充分不必要條件,求實數a的取值范圍;
(2)設命題p:“函數 ![]() 無極值”;命題q:“方程
無極值”;命題q:“方程 ![]() 表示焦點在y軸上的橢圓”,若p或q為真命題,p且q為假命題,求實數m的取值范圍.
表示焦點在y軸上的橢圓”,若p或q為真命題,p且q為假命題,求實數m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓![]() 經過
經過![]() 、
、![]() ,圓心
,圓心![]() 在直線
在直線![]() 上,過點
上,過點![]() ,且斜率為
,且斜率為![]() 的直線
的直線![]() 交圓相交于
交圓相交于![]() 、
、![]() 兩點.
兩點.
(Ⅰ)求圓![]() 的方程;
的方程;
(Ⅱ)(i)請問![]() 是否為定值.若是,請求出該定值,若不是,請說明理由;
是否為定值.若是,請求出該定值,若不是,請說明理由;
(ii)若![]() 為坐標原點,且
為坐標原點,且![]() ,求直線
,求直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知點![]() ,點
,點![]() 是圓
是圓![]() 上的任意一點,設
上的任意一點,設![]() 為該圓的圓心,并且線段
為該圓的圓心,并且線段![]() 的垂直平分線與直線
的垂直平分線與直線![]() 交于點
交于點![]() .
.
(1)求點![]() 的軌跡方程;
的軌跡方程;
(2)已知![]() 兩點的坐標分別為
兩點的坐標分別為![]() ,
, ![]() ,點
,點![]() 是直線
是直線![]() 上的一個動點,且直線
上的一個動點,且直線![]() 分別交(1)中點
分別交(1)中點![]() 的軌跡于
的軌跡于![]() 兩點(
兩點(![]() 四點互不相同),證明:直線
四點互不相同),證明:直線![]() 恒過一定點,并求出該定點坐標.
恒過一定點,并求出該定點坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】直角坐標系![]() 中,曲線
中,曲線![]() 與
與![]() 軸負半軸交于點
軸負半軸交于點![]() ,直線
,直線![]() 與
與![]() 相切于
相切于![]() ,
, ![]() 為
為![]() 上任意一點,
上任意一點, ![]() 為
為![]() 在
在![]() 上的射影,
上的射影, ![]() 為
為![]() 的中點.
的中點.
(Ⅰ)求動點![]() 的軌跡
的軌跡![]() 的方程;
的方程;
(Ⅱ)軌跡![]() 與
與![]() 軸交于
軸交于![]() ,點
,點![]() 為曲線
為曲線![]() 上的點,且
上的點,且![]() ,
, ![]() ,試探究三角形
,試探究三角形![]() 的面積是否為定值,若為定值,求出該值;若非定值,求其取值范圍.
的面積是否為定值,若為定值,求出該值;若非定值,求其取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】共享單車入住泉州一周年以來,因其“綠色出行,低碳環保”的理念而備受人們的喜愛,值此周年之際,某機構為了了解共享單車使用者的年齡段,使用頻率、滿意度等三個方面的信息,在全市范圍內發放![]() 份調查問卷,回收到有效問卷
份調查問卷,回收到有效問卷![]() 份,現從中隨機抽取
份,現從中隨機抽取![]() 份,分別對使用者的年齡段、
份,分別對使用者的年齡段、![]() ~
~![]() 歲使用者的使用頻率、
歲使用者的使用頻率、![]() ~
~![]() 歲使用者的滿意度進行匯總,得到如下三個表格:
歲使用者的滿意度進行匯總,得到如下三個表格:
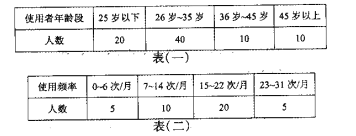
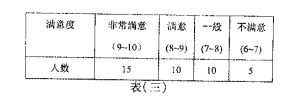
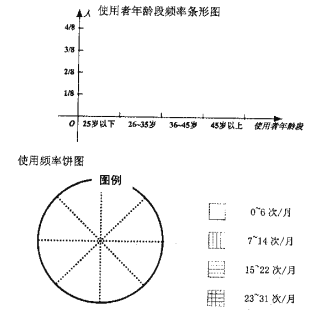
(Ⅰ)依據上述表格完成下列三個統計圖形:
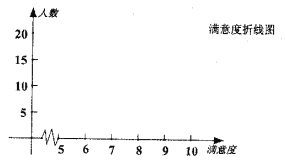
(Ⅱ)某城區現有常住人口![]() 萬,請用樣本估計總體的思想,試估計年齡在
萬,請用樣本估計總體的思想,試估計年齡在![]() 歲~
歲~![]() 歲之間,每月使用共享單車在
歲之間,每月使用共享單車在![]() ~
~![]() 次的人數.
次的人數.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com