
【題目】已知![]() .
.
(1)若![]() ,求
,求![]() 在
在![]() 處的切線與兩坐標軸圍成的三角形的面積;
處的切線與兩坐標軸圍成的三角形的面積;
(2)若![]() 在
在![]() 上的最大值為
上的最大值為![]() ,求
,求![]() 的值.
的值.
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)![]() ,求導
,求導![]() ,再求得
,再求得![]() ,得到切線方程為
,得到切線方程為![]() .再分別令
.再分別令![]() ,
,![]() ,得到在坐標軸上的截距,再代入三角形面積求解.
,得到在坐標軸上的截距,再代入三角形面積求解.
(2)![]() .
.![]() 時,
時,![]() ,故
,故![]() 在
在![]() 上單調遞增,易得
上單調遞增,易得![]() 在
在![]() 上的最大值,當
上的最大值,當![]() 時,令
時,令![]() ,得
,得![]() .再分
.再分![]() ,
, ![]() ,
,![]() 三種情況討論求解.
三種情況討論求解.
(1)若![]() ,則
,則![]() ,
,![]() .所以
.所以![]() ,
,![]() .
.
則切線方程為![]() .令
.令![]() ,得
,得![]() ,令
,令![]() ,得
,得![]() ,則切線與兩坐標軸圍成的三角形面積為
,則切線與兩坐標軸圍成的三角形面積為![]() .
.
(2)![]() .
.
(ⅰ)當![]() 時,
時,![]() ,故
,故![]() 在
在![]() 上單調遞增,
上單調遞增,
所以![]() 在
在![]() 上的最大值為
上的最大值為![]() .所以
.所以![]() .
.
(ⅱ)當![]() 時,令
時,令![]() ,得
,得![]() .
.
①當![]() ,即
,即![]() 時,
時,![]() 在
在![]() 上單調遞增,
上單調遞增,
所以![]() 在
在![]() 上的最大值為
上的最大值為![]() ,所以
,所以![]() ,舍去.
,舍去.
②當![]() ,即
,即![]() 時,
時,![]() 在
在![]() 上單調遞減,
上單調遞減,
所以![]() 在
在![]() 上的最大值為
上的最大值為![]() ,所以
,所以![]() ,不滿足
,不滿足![]() ,舍去.
,舍去.
③當![]() ,即
,即![]() 時,
時,![]() 在
在![]() 上單調遞減,在
上單調遞減,在![]() 上單調遞增.
上單調遞增.
由上面分析可知,當![]() 時,
時,![]() 不可能是最大值.
不可能是最大值.
而![]() ,
,![]() ,由
,由![]() ,可得
,可得![]() ,
,
此時,![]() ,
,![]() 的最大值為
的最大值為![]() .
.
所以![]() ,不符合
,不符合![]() ,舍去.
,舍去.
綜上可知,![]() .
.


科目:高中數學 來源: 題型:
【題目】已知拋物線![]() 的焦點為F,過F作直線交拋物線C于A,B兩點,過A,B分別作拋物線C的切線,兩條切線交于點P.
的焦點為F,過F作直線交拋物線C于A,B兩點,過A,B分別作拋物線C的切線,兩條切線交于點P.

(1)若P的坐標為![]() ,求直線的斜率;
,求直線的斜率;
(2)若P始終不在橢圓![]() 的內部(不包括邊界),求
的內部(不包括邊界),求![]() 外接圓面積的最小值.
外接圓面積的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某省從2021年開始將全面推行新高考制度,新高考“![]() ”中的“2”要求考生從政治、化學、生物、地理四門中選兩科,按照等級賦分計入高考成績,等級賦分規則如下:從2021年夏季高考開始,高考政治、化學、生物、地理四門等級考試科目的考生原始成績從高到低劃分為
”中的“2”要求考生從政治、化學、生物、地理四門中選兩科,按照等級賦分計入高考成績,等級賦分規則如下:從2021年夏季高考開始,高考政治、化學、生物、地理四門等級考試科目的考生原始成績從高到低劃分為![]() 五個等級,確定各等級人數所占比例分別為
五個等級,確定各等級人數所占比例分別為![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,等級考試科目成績計入考生總成績時,將
,等級考試科目成績計入考生總成績時,將![]() 至
至![]() 等級內的考生原始成績,依照等比例轉換法分別轉換到
等級內的考生原始成績,依照等比例轉換法分別轉換到![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 五個分數區間,得到考生的等級分,等級轉換分滿分為100分.具體轉換分數區間如下表:
五個分數區間,得到考生的等級分,等級轉換分滿分為100分.具體轉換分數區間如下表:
等級 |
|
|
|
|
|
比例 |
|
|
|
|
|
賦分區間 |
|
|
|
|
|
而等比例轉換法是通過公式計算:![]()
其中![]() ,
,![]() 分別表示原始分區間的最低分和最高分,
分別表示原始分區間的最低分和最高分,![]() 、
、![]() 分別表示等級分區間的最低分和最高分,
分別表示等級分區間的最低分和最高分,![]() 表示原始分,
表示原始分,![]() 表示轉換分,當原始分為
表示轉換分,當原始分為![]() ,
,![]() 時,等級分分別為
時,等級分分別為![]() 、
、![]()
假設小南的化學考試成績信息如下表:
考生科目 | 考試成績 | 成績等級 | 原始分區間 | 等級分區間 |
化學 | 75分 |
|
|
|
設小南轉換后的等級成績為![]() ,根據公式得:
,根據公式得:![]() ,
,
所以![]() (四舍五入取整),小南最終化學成績為77分.
(四舍五入取整),小南最終化學成績為77分.
已知某年級學生有100人選了化學,以半期考試成績為原始成績轉換本年級的化學等級成績,其中化學成績獲得![]() 等級的學生原始成績統計如下表:
等級的學生原始成績統計如下表:
成績 | 95 | 93 | 91 | 90 | 88 | 87 | 85 |
人數 | 1 | 2 | 3 | 2 | 3 | 2 | 2 |
(1)從化學成績獲得![]() 等級的學生中任取2名,求恰好有1名同學的等級成績不小于96分的概率;
等級的學生中任取2名,求恰好有1名同學的等級成績不小于96分的概率;
(2)從化學成績獲得![]() 等級的學生中任取5名,設5名學生中等級成績不小于96分人數為
等級的學生中任取5名,設5名學生中等級成績不小于96分人數為![]() ,求
,求![]() 的分布列和期望.
的分布列和期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知四棱錐![]() 的底面ABCD是邊長為2的正方形,且
的底面ABCD是邊長為2的正方形,且![]() .若四棱錐P-ABCD的五個頂點在以4為半徑的同一球面上,當PA最長時,則
.若四棱錐P-ABCD的五個頂點在以4為半徑的同一球面上,當PA最長時,則![]() ______________;四棱錐P-ABCD的體積為______________.
______________;四棱錐P-ABCD的體積為______________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,已知橢圓
中,已知橢圓![]() 過點
過點 ,離心率為
,離心率為![]() .
.![]() 分別是橢圓
分別是橢圓![]() 的上、下頂點,
的上、下頂點,![]() 是橢圓
是橢圓![]() 上異于
上異于![]() 的一點.
的一點.

(1)求橢圓![]() 的方程;
的方程;
(2)若點![]() 在直線
在直線![]() 上,且
上,且![]() ,求
,求![]() 的面積;
的面積;
(3)過點![]() 作斜率為
作斜率為![]() 的直線分別交橢圓
的直線分別交橢圓![]() 于另一點
于另一點![]() ,交
,交![]() 軸于點
軸于點![]() ,且點
,且點![]() 在線段
在線段![]() 上(不包括端點
上(不包括端點![]() ),直線
),直線![]() 與直線
與直線![]() 交于點
交于點![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下圖是某機械零件的幾何結構,該幾何體是由兩個相同的直四棱柱組合而成的,且前后,左右、上下均對稱,每個四棱柱的底面都是邊長為2的正方形,高為4,且兩個四棱柱的側棱互相垂直.則這個幾何體的體積為________.
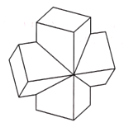
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,橢圓
中,橢圓![]() 的離心率為
的離心率為![]() ,直線
,直線![]() 被橢圓
被橢圓![]() 截得的線段長為
截得的線段長為![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)過原點的直線與橢圓![]() 交于
交于![]() 兩點(
兩點(![]() 不是橢圓
不是橢圓![]() 的頂點),點
的頂點),點![]() 在橢圓
在橢圓![]() 上,且
上,且![]() ,直線
,直線![]() 與
與![]() 軸
軸![]() 軸分別交于
軸分別交于![]() 兩點.
兩點.
①設直線![]() 斜率分別為
斜率分別為![]() ,證明存在常數
,證明存在常數![]() 使得
使得![]() ,并求出
,并求出![]() 的值;
的值;
②求![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com