
【題目】已知![]() :
:![]()
![]() ;
; ![]() :直線
:直線![]() 與拋物線
與拋物線![]() 有公共點.如果
有公共點.如果![]() 為真命題,
為真命題,![]() 為假命題,求實數
為假命題,求實數![]() 的取值范圍.
的取值范圍.
【答案】![]()
【解析】
試題分析:結合二次函數性質可求得p為真命題時的a的取值范圍,由直線與拋物線相交的位置關系可求得命題q為真命題時的a的范圍,由![]() 為真命題,
為真命題,![]() 為假命題可知兩命題一真一假,分兩種情況討論可求得a的取值范圍
為假命題可知兩命題一真一假,分兩種情況討論可求得a的取值范圍
試題解析:![]() 為真
為真![]()
![]()
![]() …………………………………………3分
…………………………………………3分
![]() 為真
為真![]() 直線
直線![]() 與拋物線
與拋物線![]() 有公共點
有公共點
由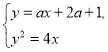 消去
消去![]() ,并整理得
,并整理得
![]() (★)……………………………………4分
(★)……………………………………4分
(1)若![]() ,則
,則![]() 方程(★)變為
方程(★)變為![]() 解得
解得![]() .
.
這時![]() 直線與拋物線有公共點
直線與拋物線有公共點![]() .
.
所以,![]() 使得直線
使得直線![]() 與拋物線
與拋物線![]() 有公共點.……………5分
有公共點.……………5分
(2)若![]() ,則
,則![]()
由直線![]() 與拋物線
與拋物線![]() 有公共點
有公共點
得方程(★)的判別式![]() ,
,
即![]() .解得
.解得![]() .
.
又![]() ,所以
,所以![]() ,或
,或![]() ………………………………………7分
………………………………………7分
綜上,若![]() 為真,則
為真,則![]() .…………………………………………………8分
.…………………………………………………8分
如果![]() 為真命題,
為真命題,![]() 為假命題,則
為假命題,則![]() 一真一假.………………………9分
一真一假.………………………9分
當![]() 真
真![]() 假時,則
假時,則![]() 或
或![]() ,且
,且![]() ,所以
,所以![]() ;…………10分
;…………10分
當![]() 假
假![]() 真時,
真時,![]() 或
或![]() ,且
,且![]() ,所以
,所以![]() .…………………11分
.…………………11分
綜上,實數![]() 的取值范圍為
的取值范圍為![]() ………………………………………12分[來
………………………………………12分[來


科目:高中數學 來源: 題型:
【題目】如圖所示,在三棱錐A-BOC中,OA⊥底面BOC,∠OAB=∠OAC=30°,AB=AC=4,BC=![]() ,動點D在線段AB上.
,動點D在線段AB上.
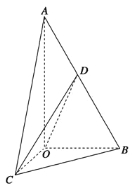
(1)求證:平面COD⊥平面AOB;
(2)當OD⊥AB時,求三棱錐C-OBD的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】以邊長為4的等比三角形![]() 的頂點
的頂點![]() 以及
以及![]() 邊的中點
邊的中點![]() 為左、右焦點的橢圓過
為左、右焦點的橢圓過![]() 兩點.
兩點.
(1)求該橢圓的標準方程;
(2)過點![]() 且
且![]() 軸不垂直的直線
軸不垂直的直線![]() 交橢圓于
交橢圓于![]() 兩點,求證直線
兩點,求證直線![]() 與
與![]() 的交點在一條直線上.
的交點在一條直線上.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com